Generalization and Safety in RL

We want to develop reinforcement learning (RL) agents that can be trusted to act in high-stakes situations in the real world. That means we need to generalize about common dangers that we might have experienced before, but in an unseen setting. For example, we know it is dangerous to touch a hot oven, even if it’s in a room we haven’t been in before.

For these common dangers, the approach we take is to learn about them in simulation in a training phase, where it is OK to experience the danger, and learn to avoid them. In order to be safely deployed, we need to generalize about these dangers in the real world.

Generalizing from a few environments

We have the following setup - the agent performs reinforcement learning on a training set of environments, and is evaluated on an unseen test set of environments, with no further training.

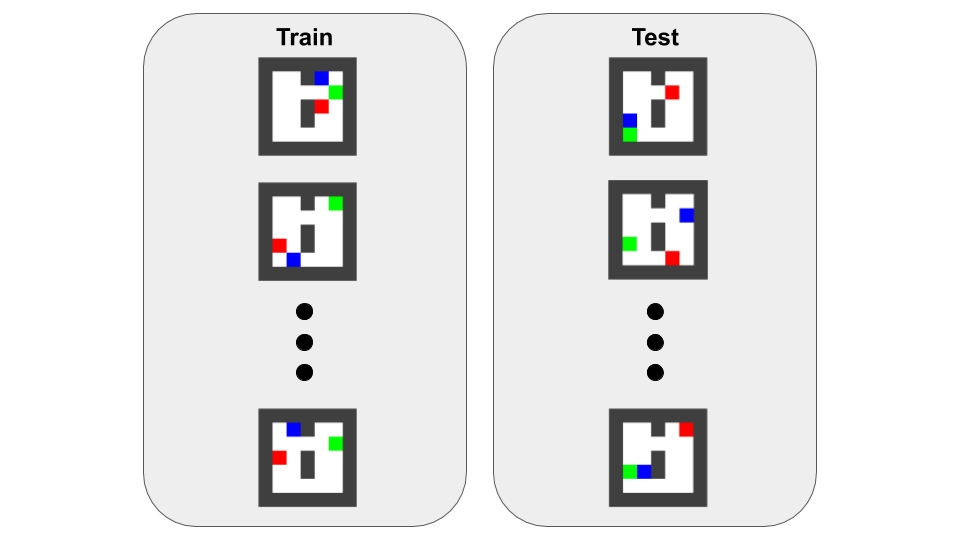
Agents tend to generalize better when trained on a wide variety of simulated training environments. Zhang et al. showed that for some gridworld environments you can get near-perfect generalization if you use a sufficient number of training environments. For more complex environments, like CoinRun , with much larger models you can also generalize well with a large number of environments.

But having a large number of simulations can be expensive! And the wider the simulation, the bigger the model needs to be to fit to it, and this big model is also more expensive to train. In this work we look at safety and generalization on a budget in deep RL. We have access to a limited number of training environments and evaluate our performance on unseen test environments. We find RL algorithms can fail dangerously on these unseen test environments even when performing perfectly on training environments.

Problem Setting

Our problem setting is as follows:

• We train on a limited number of environments and must generalize to unseen environments;
• During training, experiencing the dangers is acceptable;
• At deployment on unseen test environments, any dangerous behaviour is unacceptable.

Gridworlds

Firstly, we consider a gridworld setting, where the blue agent must uncover the map, navigating the walls, whilst avoiding the red lava and reaching the green goal.

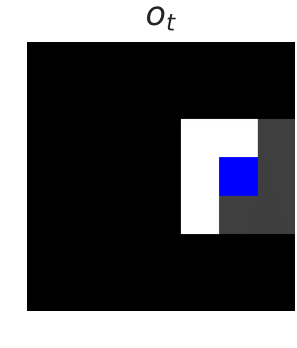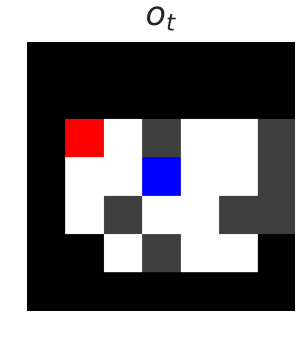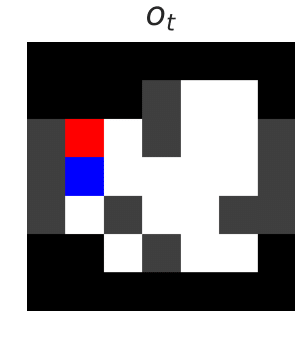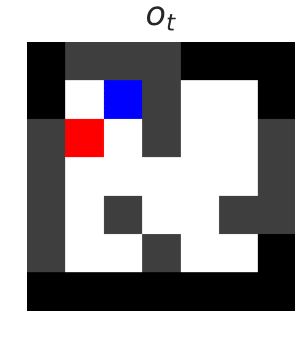
We used DQN to train our agents on gridworlds. We found that catastrophes can be significantly reduced with simple modifications, including ensemble model averaging and the use of a blocking classifier.

The following figures show visually how the blocker and ensemble help:

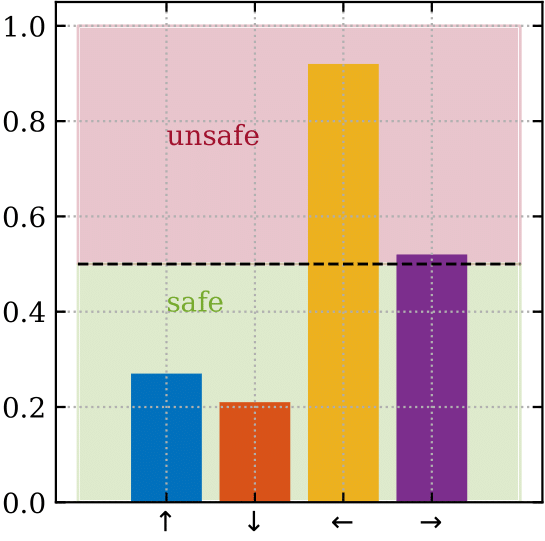
The above left figure shows the current state — moving the blue agent left in this state would be catastrophic. The above right figure shows the output of the blocker, which predicts whether an action will be catastrophic. The dashed line shows the decision threshold of 50%. If the action selected has a classifier prediction above the threshold, the blocker will block the action.

The figure below shows the 9 ensemble member’s Q-values for each action in the current state.

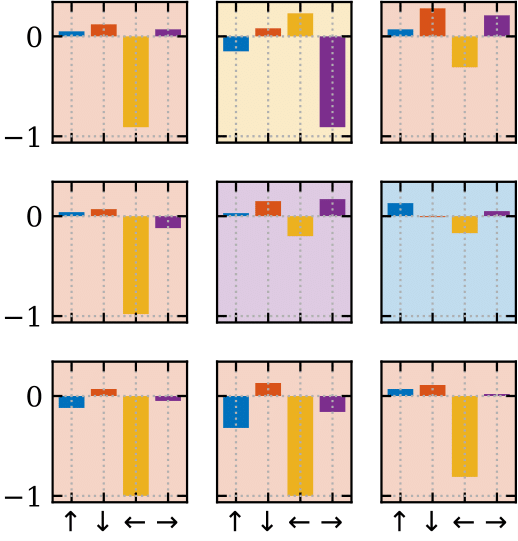
We take the mean of the Q values to produce a single mean Q value, from which we greedily take the action with the highest Q value. Taking the mean reduces the risk of a spuriously high Q value for a catastrophic action, as would be the case if we just used the top-middle member of the ensemble (which would suggest taking a left).

Our quantitative results are shown in the figure below.

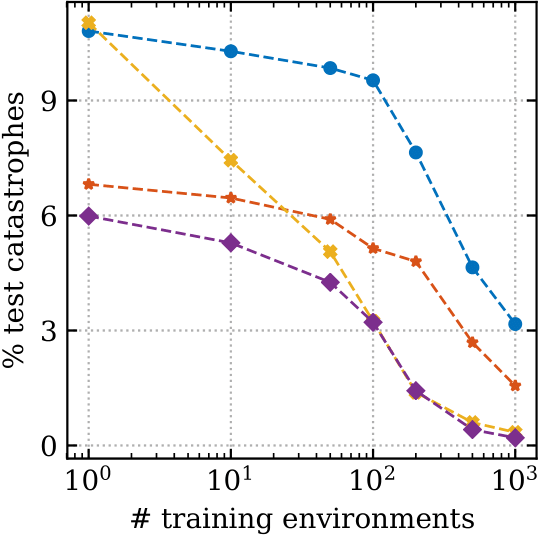
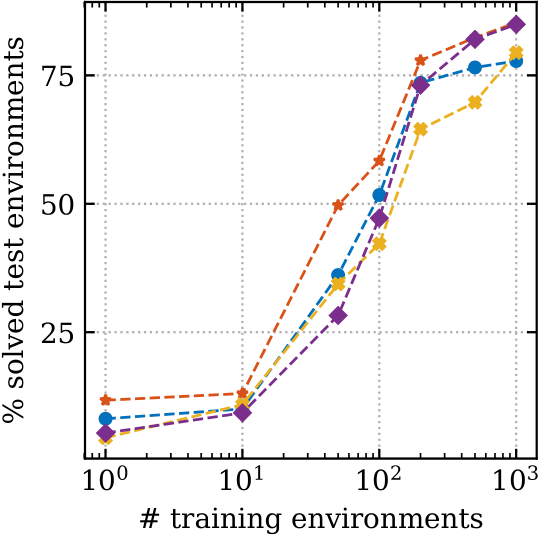
On the x-axis we show how many environments were used during training. The left plot shows the percentage of test environments that ended in catastrophe (going into the lava). On the right, we plot the percentage of test environments which were solved, reaching the goal without hitting the lava.

We see that the simple modifications help to reduce the number of catastrophes, even when only a small number of training environments were seen, and that this doesn’t harm the percentage solved.

CoinRun

We next investigated the more challenging CoinRun environment using the PPO algorithm . Here’s a gif of an agent trained on 10 environments acting on some sampled test environments: The agent has to get from its starting location to the coin, whilst avoiding the lava. The background colours and layouts change from one environment to another, whilst the lava and coin remain the same colours.

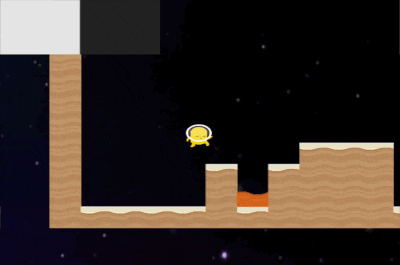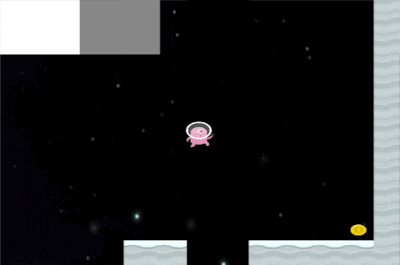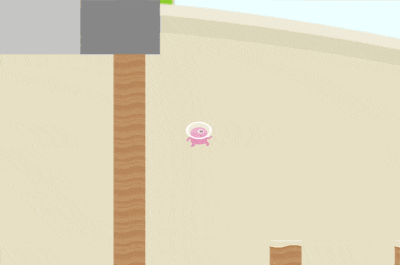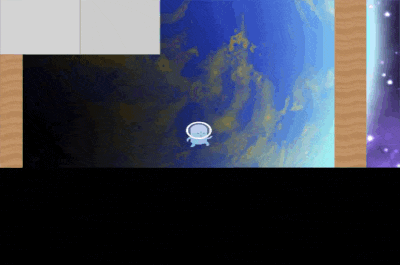
You can see it falls in the lava on one of the environments.

We trained an ensemble of five agents on different numbers of Coinrun training levels. Part of what’s harder to generalize about in this environment is the time-extended nature of the CoinRun dangers — for example, it can take about 5 agent steps for a jumping action to land in the lava, and mid-air the agent can’t do anything to change where it lands. We found that ensemble averaging methods do not significantly reduce catastrophes. We suspect that this is because the ensemble methods can decorrelate action selection across timesteps, resulting in temporally incoherent behaviour, which increases the chance of a catastrophe. This isn’t an issue in gridworlds, since the physics is instantaneous, whereas in coinrun it depends on the momentum of the agent.

However, we do find that the uncertainty information from the ensemble is useful for predicting whether a catastrophe will occur within a few steps and hence whether human intervention should be requested. We consider a binary classification task with a catastrophe occurring as the positive class. We imagine a human intervention occurring on a positive prediction, and so would like to reduce the number of false positives and maintain a high true positive rate.

An ROC curve captures the diagnostic ability of a binary classifier system as a threshold is varied — the threshold is compared to a discrimination function, which we take to be $U=\alpha \mu + \beta \sigma$. This involves the mean, $\mu$, and standard deviation, $\sigma$, of the ensemble of the five agents’ value functions. The coefficients, $\alpha$ and $\beta$, are hyperparameters. In an ROC curve, the higher the $\text{sensitivity}$ (true positive rate) and the lower the $1-\text{specificity}$ (false positive rate) the better (towards top left). The AUC score is a summary statistic of the ROC curve, the higher the better.

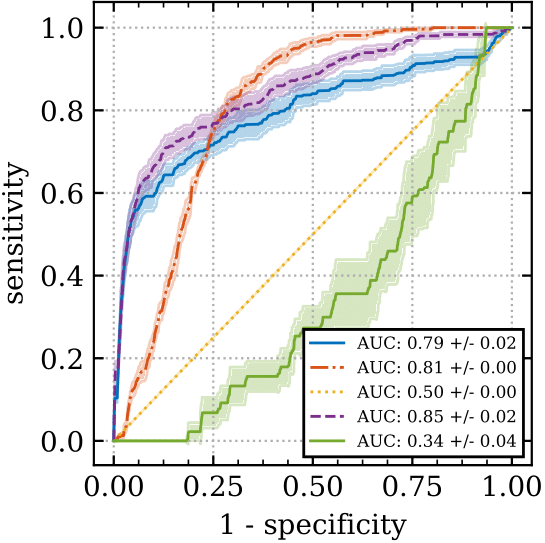
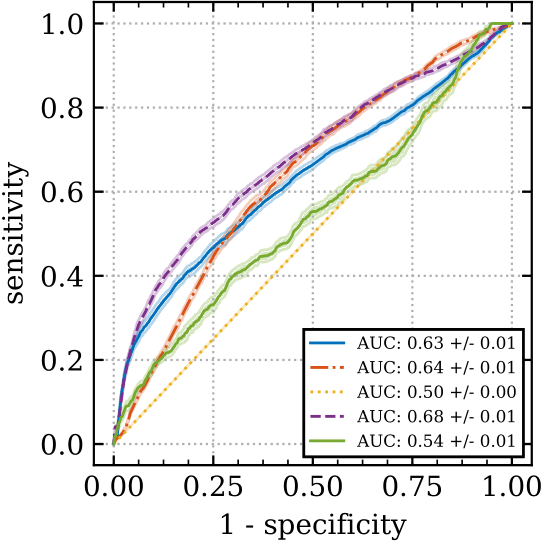
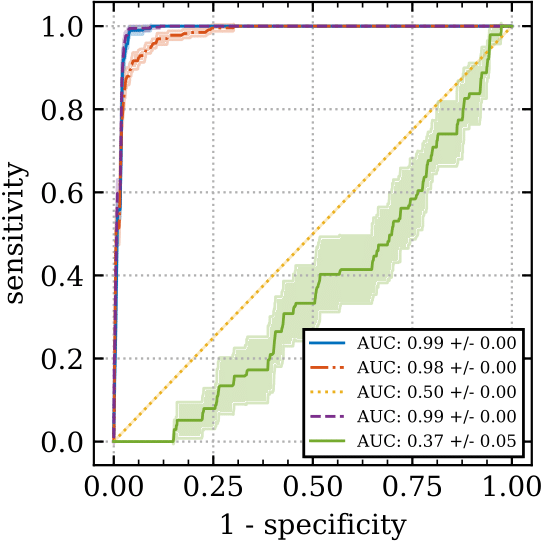
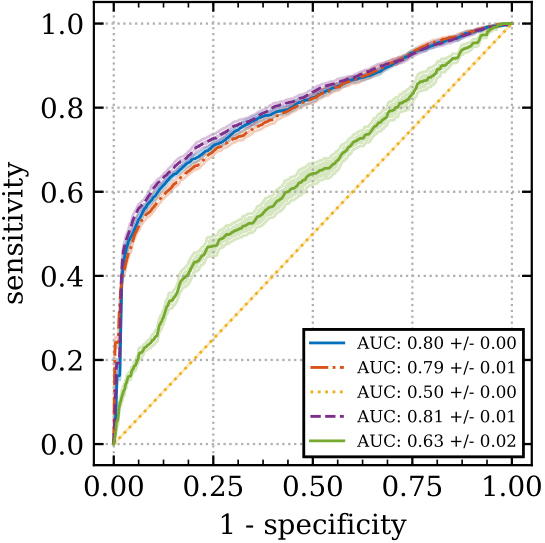
In the figure above we plot ROC curves for different action selection methods (random or ensemble-mean action selection), together with different discrimination function hyperparameters. Shown are mean and one standard deviation confidence intervals based on ten bootstrap samples from the data collected from one rollout on 1000 test environments. The top and bottom rows have 10 and 200 training levels respectively. The left and right columns have prediction windows of 1 and 10 timsteps respectively.

We see from the top left that for 10 training levels and a prediction time window of one step, the uncertainty information from using the standard deviation (purple) of the ensemble-mean action selection method gives superior prediction performance compared to not using the standard deviation (blue). However, it helps less as the time-window increases, top right, or as the number of training levels increases, bottom row. Note that it’s much easier to predict a catastrophe for a smaller time window (left column), than a longer one (right column). This supports our hypothesis that it is the time-extended nature of the CoinRun danger which is particularly challenging to generalize about.

Conclusion

In this post we investigated how safety performance generalizes when deployed on unseen test environments drawn from the same distribution of environments seen during training, where no further learning is allowed. We focused on the case in which there are a limited number of training environments. We found RL algorithms can fail dangerously on the test environments even when performing perfectly during training. We investigated some simple ways to improve safety generalization performance and whether a future catstrophe can be predicted, finding that uncertainty information in an ensemble of agents is helpful when only a small number of environments are available.