Github Website ICML Talk

In autonomous driving, we generally train models on diverse data to maximize the coverage of possible situations the vehicle may encounter at deployment. Global data coverage would be ideal, but impossible to collect, necessitating methods that can generalize safely to new scenarios. As human drivers, we do not need to re-learn how to drive in every city, even though every city is unique. Hence, we'd like a system trained in Pittsburgh and Los Angeles to also be safe when deployed in New York, where the landscape and behaviours of the drivers is different.

However, with machine learning systems this tends to be a bit more complicated. For example, when training with a dataset, there are no guarantees about the performance of the trained system on inputs that are significantly different to the ones encountered during training, a case commonly termed out-of-distribution scenario or distribution shift.

In this project, we propose a solution to the out-of-distribution problem in the imitation learning setting, where an expert provides demonstrations of successful driving experiences. Additionally, we propose a method for quickly adapting in cases where the driving agent encounters novel scenes as well as a way of identifying such out-of-distribution scenes and warn the driver.

Planning Under Uncertainty

But first, let’s describe the uncertainties involved in machine learning systems. First we have to disentangle between the aleatoric and epistemic uncertainty. Aleatoric uncertainty is commonly referred to the uncertainty caused by lack of information, either because of noisy sensory input or incomplete knowledge. As an example, one can think of deciding whether to go left or right in a junction. Both actions can be equally valid however one can only decide once the goal is set, in which case the uncertainty is reduced after additional information is provided to the decision maker.

On the other hand, epistemic uncertainty is the subjective uncertainty with respect to the trained models. It’s what the models know they don’t know. The important thing with epistemic uncertainty is that it can be reduced once more training data are available.

Our method is disentangling the aleatoric and epistemic uncertainty but focuses on the epistemic uncertainty to identify distribution shifts and also provide safer plans under uncertainty.

But first, let’s appreciate the importance of this issue and our solution with an instructive example.

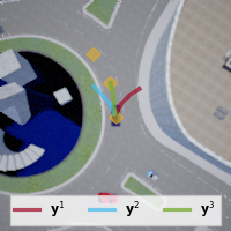
The two figures illustrate the failure of a current state-of-the-art method to drive safely in novel scenes. As we see on the picture on the left, models trained on different samples of the same data can exhibit abnormal behaviour when asked to drive in out-of-distribution. In our project, we base our work on Deep Imitative Models where they learn distribution over the possible future trajectories and to plan they select a trajectory that maximizes the likelihood. As we can see on the table, when our agent is out-of-distribution, we have no guarantee that the maximizing trajectory is the best to follow. This demonstrates a failure case because of high epistemic uncertainty.

Given that we have multiple trained models, can we suggest a better trajectory? What if instead of throwing away the information from the different models, we were aggregating their evaluation before we plan?

In this example, we see that if we take the minimum over the likelihood evaluated by the different models and select the trajectory that maximizes this instead, the resulting trajectory is safer than the one suggested by a single model, on expectation.

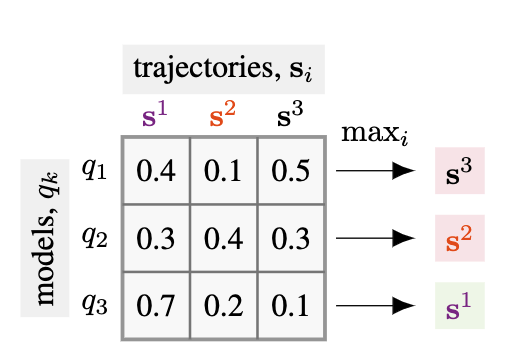
But why is this a better objective to use? Although this may seem surprising at first, this is inspired by robust control theory [2] and incorporates epistemic uncertainty [3] while planning, instead of only the aleatoric uncertainty which is inherent in the dataset. Our method, termed Robust Imitation Planning, formalizes the “evaluate”, “aggregate” and “plan” loop which is incorporating the epistemic uncertainty exposed by the different models trained on the same data, a technique commonly termed Deep Ensembles.

Robust Imitative Planning and Evaluate Aggregate Plan

Our work, based on top of Deep Imitative Models , uses the likelihood model of the future trajectories, which we term imitation prior, and also a second likelihood term called goal likelihood which allows us to plan goal conditioned trajectories. Deep Imitative Models, follow the evaluate and plan paradigm.

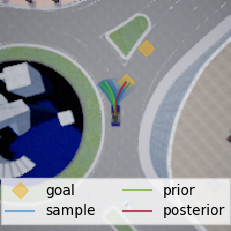
It is very important to highlight two points here that distinguish our contributions from prior work:

1. we maintain a subjective belief of the model parameters, i.e., model posterior, which induces a predictive distribution over trajectories, enabling the detection of distribution shifts. this is in contrast to simple probabilistic models that capture only the aleatoric uncertainty inherent in the training data.
2. by capturing epistemic uncertainty at the evaluate step, we enable the aggregation before planning.

This extra step of aggregation before planning introduces epistemic uncertainty awareness to the system.

The objective is shown below $$ \begin{align} y^{\mathcal{G}}_{\text{RIP}} \!&\triangleq\! \arg max_{y} \overbrace{\underset{\theta \in \text{supp}(p(\theta | \mathcal{D}))}{\oplus}}^{\text{aggregation operator}} \; \log \underbrace{p(y | \mathcal{G}, x;\theta)}_{\text{imitation posterior}} \nonumber \\ \!&=\!\arg max_{y} \underset{\theta \in \text{supp}(p(\theta | \mathcal{D}))}{\oplus} \! \log \!\underbrace{q(y|x;\theta)}_{\text{imitation prior}} \! + \log \!\!\!\!\! \underbrace{p(\mathcal{G}|y)}_{\text{goal likelihood}}, \label{eq:generic-objective} \end{align} $$

In this project, we explored two different aggregation operators:

1. The Average Aggregation is inspired by the Bayesian decision theory where the evaluation of each model is weighted by its posterior probability.
2. The Worst Case Aggregation uses the min operator and its intention is to improve the performance according to the worst case likelihood.

Practical Implementation

As we have already hinted, this can be easily implemented using Deep Ensembles or MC-dropout for modeling the epistemic uncertainty. But in practice, any other bayesian or non-bayesian inference method that enables quantification of the epistemic uncertainty is compatible with RIP and can be used instead.

At a given scene, such as x illustrated at the figure above, we start from a random trajectory y and we run the “evaluate” step with the deep imitative models, feed-forwarding the context x and the trajectory y through the ensemble, as depicted in yellow (c). Having selected which aggregation operation we want to use, we aggregate the evaluation at the green layer. In the case of deep ensembles, the aggregation over the finite number of models can be trivial implemented. Lastly, since all the aforementioned operations are differentiable, the gradients with respect to the trajectory can be computed and gradient-based optimization methods can be used to optimize the RIP objective.

Below we can see a simple implementation in pytorch. Alternatively, feel free to check the full implementation here https://github.com/OATML/oatomobile/

def robust_imitative_planning(x, goal, imitative_models):
  T = 8  # length of plan.
  N = 20 # number of gradient steps per plan.

  # Starts from a random plan.
  y = torch.randn(T, 2)

  # Gradient-based online planner.
  optimizer = optim.Adam([y], lr=1e-3)

  # `EVALUATE`-`AGGREGATE`-PLAN` loop.
  for _ in range(N):

    ##############
    ## EVALUATE ##
    ##############
    # Evaluates plan `y` under imitation models.
    imitation_posteriors = list()
    for model in imitative_models:
      imitation_posterior =
            model.imitation_prior(y, x) + \
            model.goal_likelihood(y, goal)
      imitation_posteriors.append(imitation_posterior)

    # Aggregate scores from the `K` models.
    imitation_posteriors = torch.stack(
                  imitation_posteriors, dim=0)

    ###############
    ## AGGREGATE ##
    ###############
    # Choose one of RIP variants.
    if self._algorithm == "WCM": # worst case model (pessimism)
      loss, _ = torch.min(-imitation_posteriors, dim=0)
    elif self._algorithm == "BCM": # best case model (optimism)
      loss, _ = torch.max(-imitation_posteriors, dim=0)
    else: # model average (marginalisation)
      loss = torch.mean(-imitation_posteriors, dim=0)

    ##########
    ## PLAN ##
    ##########
    # Backward pass.
    loss.backward(retain_graph=True)
    # Performs a gradient descent step.
    optimizer.step()

  return y
    

Quantitative Results

But how does RIP do in practice? We evaluate our method on two settings: nuScenes, a real-world dataset, which consists of rich offline data from boston and singapore and CARNOVEL, a suite of driving tasks based on the CARLA simulator, developed for benchmarking out of distribution driving scenarios.

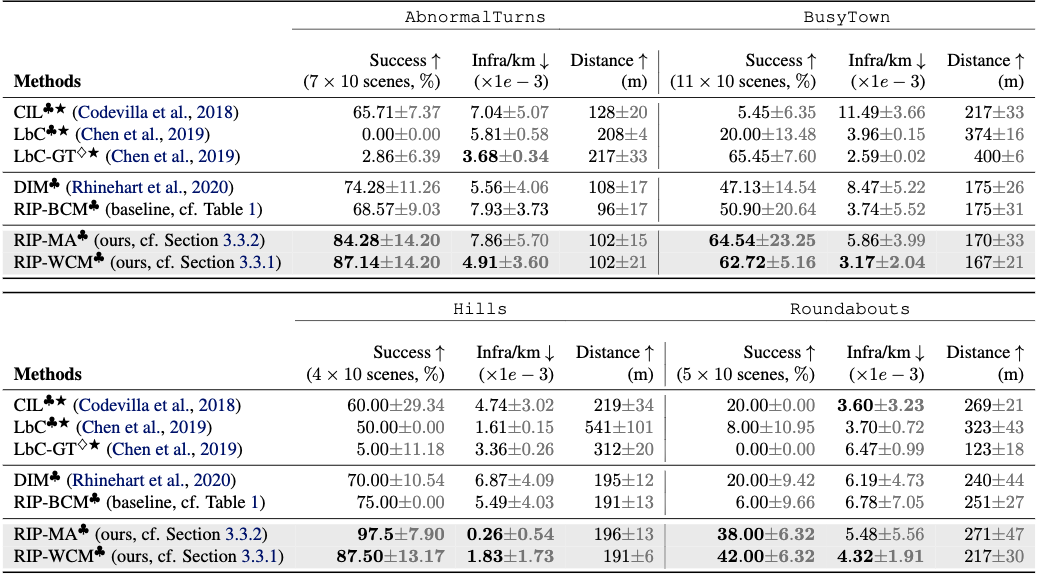
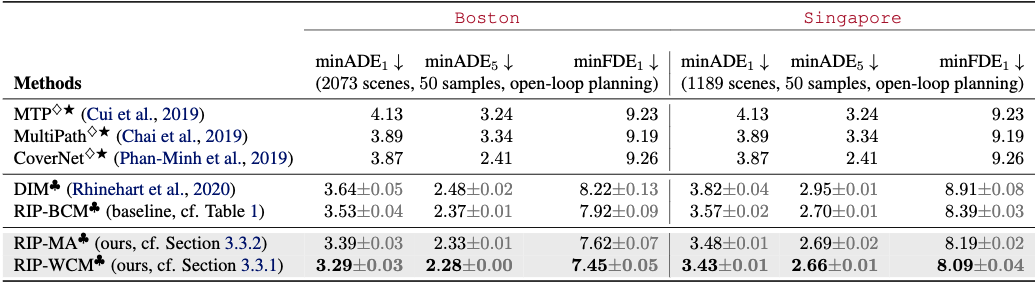
As seen on the tables above, our method outperforms uncertainty-unaware baselines and demonstrates safer behaviour as measured by the distance travelled without infractions.

AdaRIP

We showed that RIP can perform well under epistemic uncertainty however this is still far from driving safely. A natural question is, can we do better? Our final contribution is to propose a method of adapting to novel scenes, assuming we have access to an expert that we can access at driving time.

The proposed method, termed Adaptive Robust Imitative Planning or AdaRIP for short, uses the predictive variance as an indicator for out-of-distribution scene to ask the expert for input. Next it updates the model to adapt on-the-fly, without compromising the safety of the driver.

In the figure below, we depict trajectories before and after adaptation as well as models’ uncertainty from low in white to high in red.

Conclusion & Open Research Questions

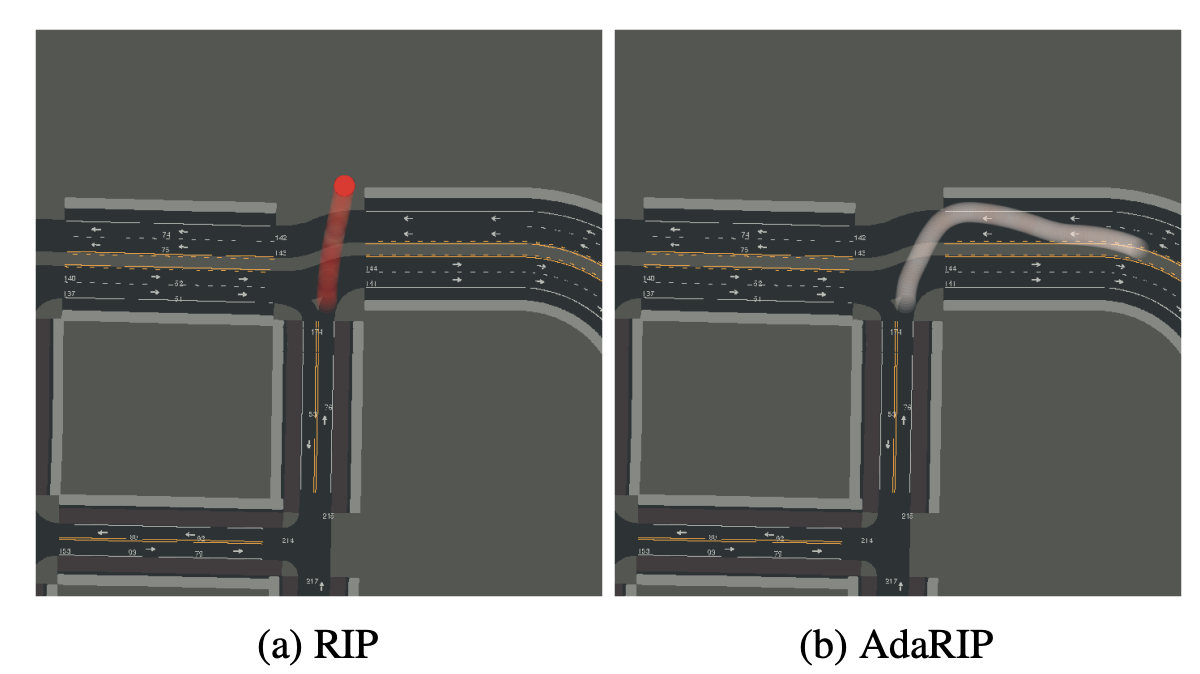
To summarise, in this paper we posed the following question: Can Autonomous Vehicles Identify, Recover From, and Adapt to Distribution Shifts?

We answer these questions by introducing a detection mechanism based on epistemic uncertainty quantification, we improve existing imitation learning methods by introducing an epistemic-uncertainty-aware objective termed RIP and we presented an adaptive variant, AdaRIP, which uses epistemic uncertainty to efficiently query the expert for input and adapt quickly without compromising safety at deployment.

Finally, we released the codebase and a benchmark for the community to use and develop additional uncertainty aware models.

Unfortunately, there is a lot to be done until we can safely solve the autonomous driving problem. With this work we identified several open questions, some of which are actively researched. For example:

1. In time critical situations, querying multiple models might be prohibitive. Can we do real-time epistemic uncertainty estimation?
2. Additionally, real-time planning with models that capture aleatoric and epistemic uncertainty still lag behind their deterministic counterparts. To achieve competitive performance, additional tolling is required.
3. Finally, although we demonstrated a direction for online adaptation there are still open questions on how we can adapt without catastrophically forgetting, with just a handful of examples and without sacrificing safety and performance.