Are capsules a good idea? A generative perspective

I’ve recently written a paper on a fully probabilistic version of capsule networks. While trying to get this kind of model to work, I found some interesting conceptual issues with the ideas underlying capsule networks. Some of these issues are a bit philosophical in nature and I haven’t thought of a good way to pin them down in an ML conference paper. But I think they could inform research when we design new probabilistic vision models (and they are very interesting), so I’ve tried to give some insight into them here. This blog post is a companion piece to my paper: I start by introducing capsules from a generative probabilistic interpretation in a high level way, and then dive into a discussion about the conceptual issues I found. I will present the paper at the Object Oriented Learning workshop at ICML on Friday (July 17), so do drop by if you want to chat.
What are capsule networks
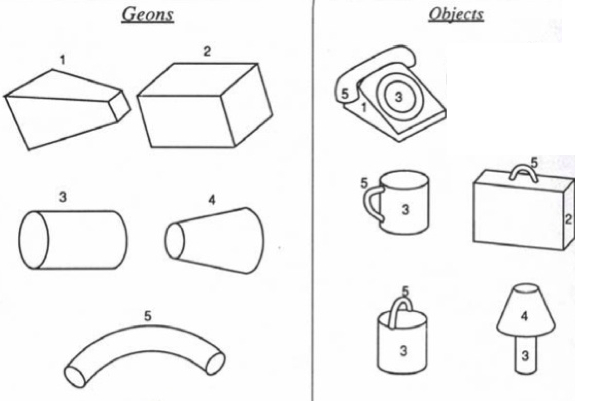
On the left, a set of simple ‘geons’, proposed recognisable simple objects from the psychological theory of ‘recognition by components’ theory. On the right, how various complex objects can be represented as arrangements of the geons.
Capsule networks aim to explicitly represent objects and their instantiation parameters, like position, size, and so on. What do we mean when we say that we want to represent objects? After all, normal neural networks must have some representation of objects in order to be able to classify them. Broadly speaking, convolution networks learn feature detectors which are scanned over the image, with more abstract feature detectors working on the outputs of earlier ones. There is a good visual overview and investigation of this in this Distill article. But while feature detectors in CNNs correspond to objects, the information is place-coded - that is, information about what objects are is encoded in which units are active, and information about that object position is also place coded by the location in a feature map where that unit is activated. In contrast, a ‘rate-coded’ neuron would have only the object identity coded by place, and would represent attributes of the object like the position via a numerical vector. A simple way, for instance, to move from a ‘place coded’ to a ‘rate coded’ representation of position is to take the arg-max across spatial dimensions of an activation map.
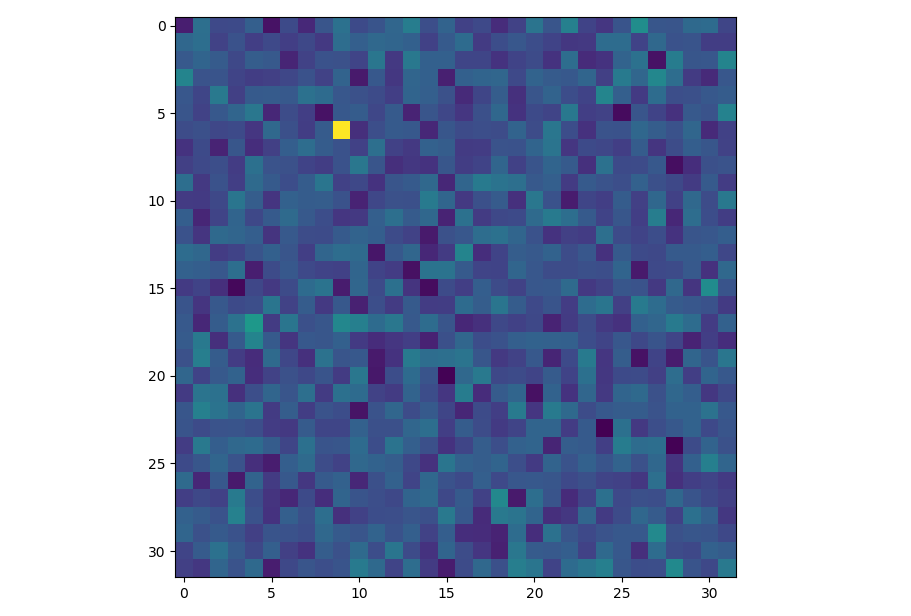
An example of place coded information in a feature activation map. The position of an object is represented implicitly by the location of a highly activated unit. A rate coded representation of this information would be the position vector \((-0.63,-0.43)\) which describes the position of this activation relative to the centre of the image.
So by explicitly representing objects, we mean having a model which may place code object identity, but rate codes other information like object position, orientation, colour and so on. There are other models that instantiate objects. Representative examples include Attend, Infer, Repeat and MONet, which represent instantiation parameters of objects in a fixed number of exchangeable ‘object slots’1. In addition to rate coding information, capsules try to capture a notion of compositionality - that is, of more complex objects being composed of geometrical arrangements of simpler objects. Models like AIR and MOnet don’t have this - they map directly from pixels to objects rather than building up objects out of simpler objects.
The picture of building objects out of a set of simpler components is similar to (and quite possibly originally directly inspired by) the psychological concept of geons, which are pictured above. The idea being that the brain can recognise a set of simple objects (the geons, on the left hand side) which are recognisable in a wide variety of orientations, and objects are recognised by recognising arrangements of these shapes. For example, if we have ‘slots’ in our model that represent the instantiation parameters, like the pose, deformation, and presence of the objects on the left, then we can recognise the objects on the right in terms of relations between these instantiation parameters. In high level terms, something along the lines of ‘a cup is present when object 5 and object 3 are present, and their instantiation parameters \(x_5\) and \(x_4\) stand in relation \(R\) to one another’. I am very much not qualified to comment on the biological plausibility of this theory, but the idea would be that compared to the feature detectors in normal CNNs, a rate coded representation could be far more efficient.
To be more concrete about what relation \(R\) we expect to find, we need to talk a bit about pose. The instantiation parameter of these lower level objects we particularly want to capture with capsule networks is the affine pose. What I mean by the pose is that, to represent the position of an object, we can describe it in terms of a transformation from some particular reference position. All position co-ordinates are really just describing transformations - the \((x,y)\) Cartesian co-ordinate system describes the translation to get to a particular position relative to an arbitrary reference point (the origin) which is given co-ordinates \((0, 0)\). An affine pose is an affine transformation from a reference co-ordinate frame, and has 6 degrees of freedom in 2D.
Affine transformations include rotations, scalings, translations and shear. There are other kinds of transformation of objects that aren’t representable by an affine transform: deformations, changes in colour and texture, etc. Our notion of when two objects are ‘the same object, related by a transformation’ and ‘two different objects’ depends, of course, on what transformations we consider2. If we allow very flexible transformations, like homeomorphisms, then we end up with a very broad notion of what ‘the same object’ is.3

A transformation between a coffee cup and a donut. Are these different objects or the same object with different instantiation parameters? (Image from Wikimedia commons.)
Instead, we want to consider a restricted set of transformations, which will give us a weaker notion of equivalence between objects, but hopefully will have other representational advantages. In particular, we want to consider affine, or linear, transformations of objects. Affine transformations are a tempting choice for a couple of reasons. Firstly, they can be represented as small matrices with 6 degrees of freedom, and the application of the transformation as matrix multiplication, which is obviously convenient. Secondly, they have a physical motivation; consider a picture drawn on a flat wall. If we assume that the wall is large enough that we can’t see around it, so we can discount effects from depth or objects behind the wall, and assume that lighting is constant, then any images taken of the wall by a camera at different positions are affine transformations of each other.4 So affine transformations are related to the transformations between images caused by changes in perspective. This is why we might think that this would be a useful equivalence between objects for computer vision, as it gives us a bias to represent an object seen from two different camera angles as ‘the same’.
Another reason to consider affine transformations is that they are an attractive candidate for the ‘relation between objects’ that we want to use to build up a description of higher level objects out of lower level ones. If an object is a geometrical arrangement of simple objects, then we can describe our ‘high level’ object as a list of affine poses of the simple objects it contains. So, for instance, we might say that a cup (in an arbitrary canonical position) consists of object 5 in pose \(M_5\) and object \(3\) in pose \(M_3\). If we now allow the high level object to also have a pose-based description, then the relationship between the pose of the parent and the pose of the child is linear - if the pose of the parent is \(A\), then the corresponding pose of the child is \(AM\) - first transform the object to its position in the canonical orientation (\(M\)), then transform the whole thing by the pose of the parent object \(A\), exploiting the fact that affine transforms can be composed by multiplying matrices.
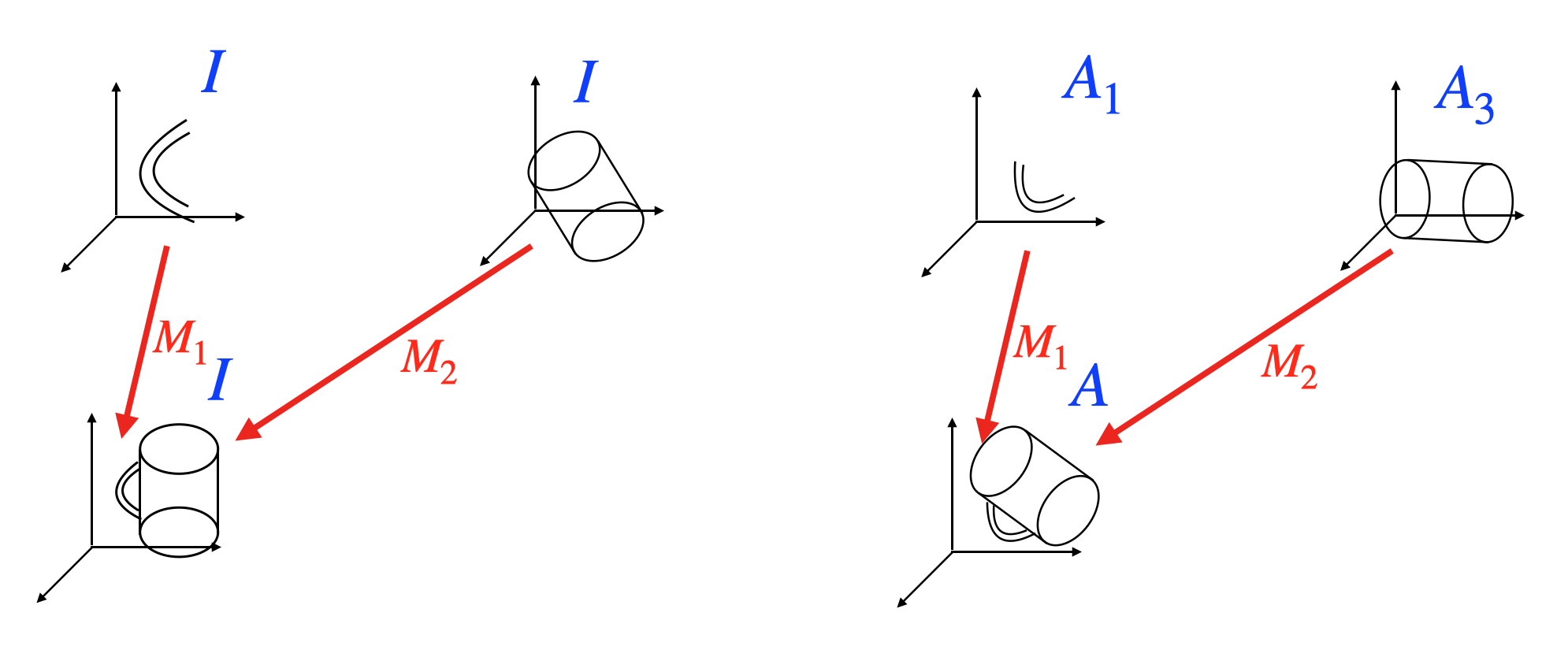
A pictorial representation of the relationship between objects and parts. In a canonical orientation of the object, where its ‘pose’ is the identity matrix, the position of the parts relative to their canonical orientations are given by transformation matrices \(M\). If the top level object is transformed by \(A\), then the relationship between the parts is invariant.
The reason we might be excited about this is that we have a relationship which is both invariant to position and linear, which means that we can have fantastic generalisation if we can capture it correctly; if we can learn the relationships \(M\) that describe an object in one position, we now know how to describe it in any affine position as well! In practice, formalising a model that takes advantage of this intuition turns out to be fairly challenging, but now we describe our attempt to do so.
A generative picture
The picture we drew in the section above about objects and their relationships has a generative flavour to it - once we know the pose of a top level object and whether it is present, we know how to arrange all of the low level objects that make it up. This suggests writing this down as a generative model, where we describe the model in terms of conditional distributions over child poses given parent poses (and similarly for presences, etc.). Interestingly, most of the capsule papers that I feel got the most attention, namely those building on the dynamic routing paper by Sabour et. al, were discriminative, and based around trying to use a clustering algorithm as a kind of novel, unusual activation function. Hopefully we will see how you might get this kind of clustering algorithm out of a generative viewpoint as we go.
What should this generative model look like? It’s probably helpful to introduce some notation here. Let’s say we have a set of high level objects, indexed by \(i\), and a set of simple objects, indexed by \(j\). For concreteness, you can imagine that these are the objects in the geon diagram earlier in this post - the simple objects on the left indexed by \(i\) and the complex objects on the right by \(j\). Going with terminology from graphical models, we might also describe the complex objects as the ‘parents’ and the simple objects that make them up as the ‘children’ of that parent.
We know that we want the high level objects to have a pose \(A^p_i\) (\(p\) for parent, \(i\) for which parent). We probably also need to include a variable that tells us whether a particular object is present or not - let’s call that \(t^p_i\). (It would be nice to call it ‘\(p\)’ for presence, but unfortunately probability and parent also start with p). We can imagine that, when sampling a scene, we randomly decide these properties of our high level objects from some arbitrary prior distribution - for example,
\[t_i^p \sim \textrm{Bernoulli}(1/n_{objects}) \\ A_i^p \sim \textrm{Normal}(I, 1) \\\]Notice that we draw \(A_i^p\) from a distribution centred around the identity matrix rather than zero - this is because we want the ‘default’ position to be the canonical orientation of the object. \(A_i^p\) is the affine matrix representing the pose of the object.5 In reality we may want to put more detailed priors, including interactions between the parent objects or similar, but this will do for now conceptually.
Now, how do we determine the poses of the children? Of course, if we know that object \(j\) belongs to parent \(i\), then we know that its pose should be centred on the parents pose \(A_i^p\) transformed by the corresponding relative pose \(M_{ij}\), following our argument earlier. But how do we decide which parent a simple object belongs to? One solution is to have a fixed number of object ‘slots’ in the model, and have each object choose which parent it belongs to. It may be possible to allow children or parents to be repeated multiple times in the same image, but this complicates things significantly. With fixed numbers of objects, we can give each simple object a selection \(s_{j}\) variable encoding this; a categorical which can take the values \(\{1..n_{objects}\}\). Clearly, a simple object can only be part of a parent object which is actually present, and we can introduce some extra parameters \(\rho_{ij}\) to represent the prior probability that that child is explained by that parent
\[P(s_j = i \mid t^p_1, t^p_2, t^p_3,...) \propto \rho_{ij} t^p_i\]Once we know which complex object is responsible for the simple object, its pose should be centred on the pose of the parent, transformed by the corresponding parent-child relative pose;
\[p(A_j \mid A^p_i, s_j=i) = \textrm{Normal}(A^p_i M_{ij}, \lambda_{ij})\]And we also need to put a distribution over its presence. The affinity parameter can play a double role here - \(P(t_j \mid s_j=i) = \textrm{Bernoulli}(\rho_{ij})\).
This simple sketch gives us a model that kind of resembles a mixture of Gaussians, with the parents playing the roles of the cluster means and the children playing the roles of the points, only with separate transformation parameters for each point. It’s also a model that was (kind of) used in the capsule paper on EM routing, though in that paper it wasn’t written out explicitly. But an algorithm similar to the EM routing algorithm presented in that paper can be derived explicitly from this model by deriving an EM procedure to infer the maximum likelihood solution for the parent poses and presences conditioned on the child poses and presences. In broad terms, the EM routing paper uses this procedure as a non-linearity between layers, but this doesn’t correspond to any global generative model.
We can also easily extend this model to a sequential hierarchy of objects, with level one objects made out of simple objects, level 2 objects made out of level 1 objects, and so on. One fairly obvious problem, though, is the fact that we are rarely presented with the direct poses of objects as input - instead, we see a scene represented as an array of pixels. So our model needs to be somehow connected to the pixel space in order for us to do anything with it.
Here, the picture becomes slightly ugly. We run a few issues here - first, we want to force the model to separate pose and other aspects of appearance, but at least for standard network architectures, it is difficult to correctly infer the pose 6. Secondly, if our model is flexible, then we introduce identifiability issues between explaining variations using pose and using the rest of the models latent space. For instance, if we give the lowest level objects a VAE style setup, so that they have both a pose variable and a latent code for appearance, then the model may learn to always set the pose to an arbitrary value and explain all visual variation with the latent code. It may be possible to get around this problem with careful enough design, but when exploring this kind of model, a simple fix is to simply make the template model very simple. The simplest possible thing to do is to associate every lowest level ‘part’ with a small, fixed image template. In this case the model is forced to use the pose variable in order to modify the appearance of parts. To draw an image, we transform every patch by the pose variable of that capsule and composite them into the final image (if the patch’s presence variable is on) using alpha compositing.

Top - two images of a three reconstructed by our capsule model, with the different parts patches coloured in differently (the actual images are grey) for visualisation. We can see that the model uses the same patches to draw corresponding parts of the digits, at least in this example. Below, all the templates learned by the model.
Again, this model is extremely restrictive, and unlikely to really scale to realistic data. However, even with this, we find some flaws with the way this kind of model operates.
But in any case, this gives us at least a model with which to work. With a template model for the lowest level objects, we can proceed to write down a joint probability for the entire model. Once we have a joint probability, we can derive a variational lower bound, and proceed to use that as an objective for training an amortised inference network which will give us our posterior over the latent variables conditioned on an image, similar to a VAE encoder. In practice, we implement our model with the probabilistic programming language pyro. There are a few important implementation details that I’m skipping over here, especially how we deal with the discrete variables in the model and the architecture in the encoder, but I don’t want to get any more bogged down in the details than I already have done - you can consult the paper for more details if you are interested.
There are a few ways to train this kind of model. In our paper, we explore unsupervised training, although in principle we could look into other paradigms; if you were willing to enforce an explicit association between top level objects and labels, for example, you could get this kind of thing to do semi supervised learning or similar.
Do capsule networks deliver?
Recall that the aim of capsule networks, and largely the experimental criterion on which they are evaluated, is generalisation to unseen viewpoints, or transformations of data not seen during training. As mentioned, the logic behind this is that the linearity of the relationship between the pose of a part and the pose of an object, given the learned object-child transformation matrices.
We can evaluate our model in this setting, and we find that we get comparable performance to other unsupervised capsule methods on MNIST and Affnist, a dataset consisting of MNIST augmented by mild transformations.
| Rotated MNIST | Affnist | |||||
|---|---|---|---|---|---|---|
| Max \(\theta\) | \(0\) | \(45\) | \(90\) | \(135\) | \(180\) | - |
| \(t^0\) | \(0.96 \pm 0.01\) | \(0.78 \pm 0.02\) | \(0.56 \pm 0.02\) | \(0.47 \pm 0.01\) | \(0.44 \pm 0.01\) | \(0.88 \pm 0.03\) |
| \(t^0, A^0\) | \(0.97 \pm 0.00\) | \(0.90 \pm 0.01\) | \(0.77 \pm 0.01\) | \(0.69 \pm 0.01\) | \(0.65 \pm 0.01\) | \(0.92 \pm 0.03\) |
| VAE | \(0.94 \pm 0.00\) | \(0.69 \pm 0.01\) | \(0.44 \pm 0.01\) | \(0.35 \pm 0.01\) | \(0.34 \pm 0.00\) | \(0.40 \pm 0.01\) |
Table: Classification results on latents for models trained on normal MNIST, showing generalisation to rotations and affine transformations (Affnist). \(t^0\) means classification based only the top level presences, and \(t^0, A^p\) means we are also allowed to use the pose. The VAE is a simple baseline to show how a non-pose-aware model performs. Probably you could do a bit better in terms of raw numbers by messing with the VAE arch. but the trend is clear.
However, Affnist is actually not a very strong test of generalisation to novel viewpoints, as it only contains rotation up to about 20 degrees, and similarly minor shifts in scale and shear. But in principle, our generative model here can express any object that it has learnt in any affine transformation whatsoever, which is why we also test with rotations up to 180 degrees. Of course, at this point we would expect the performance to fall off somewhat, not least because some MNIST digits become difficult to distinguish at this rotation (6’s and 9’s are near affine transformations of each other.)
But we shouldn’t necessarily expect that our model will generalise in this test since we are using amortised (neural encoder) inference, so even if the generative model generalises, our encoding procedure might not work on out of distribution data. One way to test if this is the only cause is to see what happens when we train the model on this kind of augmented data. If capsules are going to help us generalise to unseen transforms, we should expect that they should also help if we have those transformations in the training set.
Interestingly enough, though, we don’t really see this. Here is a graph of performance for the model trained on augmented data as we increase the degree of rotation;
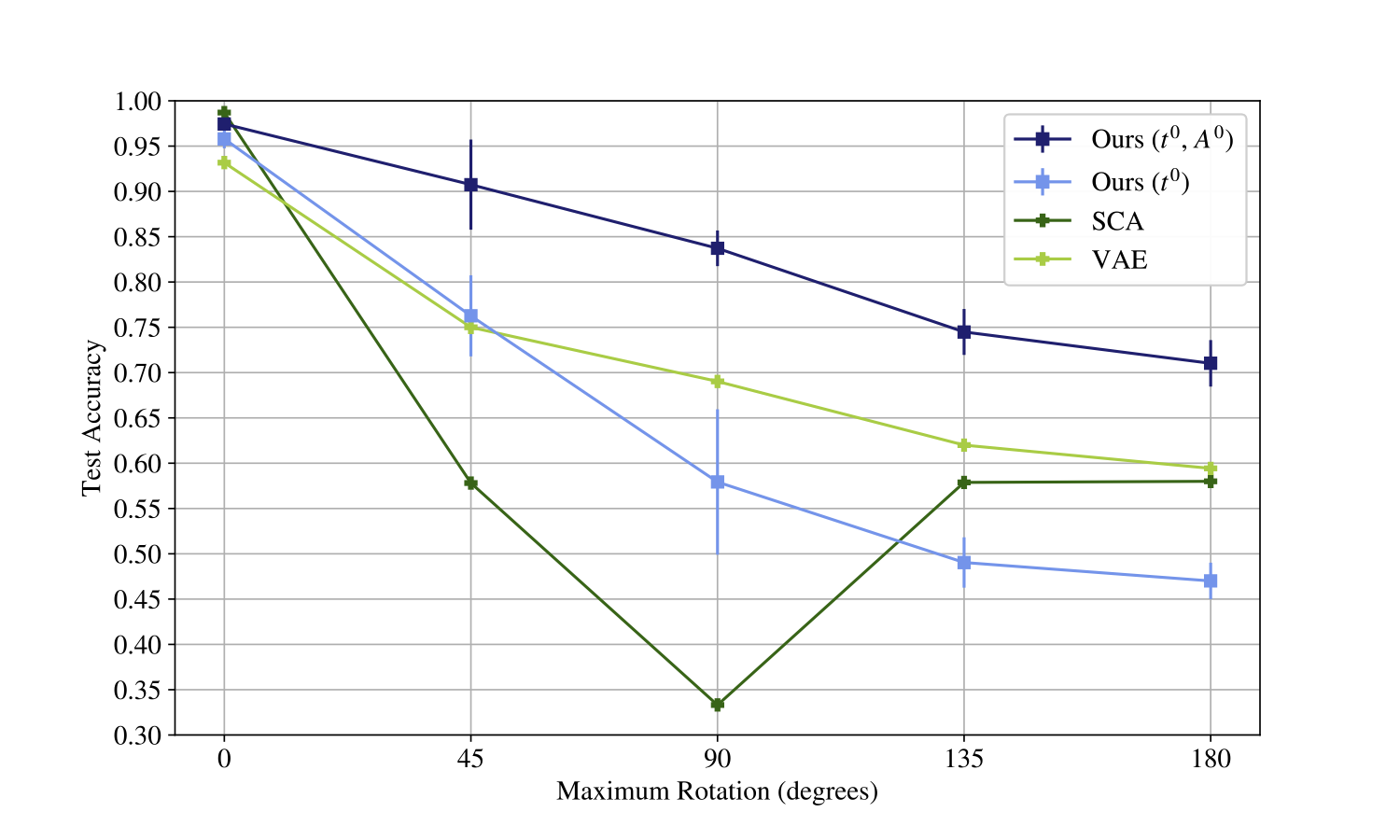
Performance of classification based on the latents for models trained on MNIST augmented by rotations up to 180 degrees. Note that in this case, rather than the previous table, these augmentations were added to the training set. Despite this, we still see a big degradation in performance as we increase the rotational budget.
To check that this isn’t specific to our experimental setting, we also perform this experiment with the Stacked Capsule Autoencoder, a capsule formulation which is closely related to our work, though not explicitly probabilistic. We see a similar effect, which we think is evidence that this is an issue with the broader model and not our specific implementation of it.
As we can see, in this situation, neither our model or the SCAE looks particularly good. We can get a feel for what’s going on by visualising the model’s reconstructions for images with a large difference in orientation;
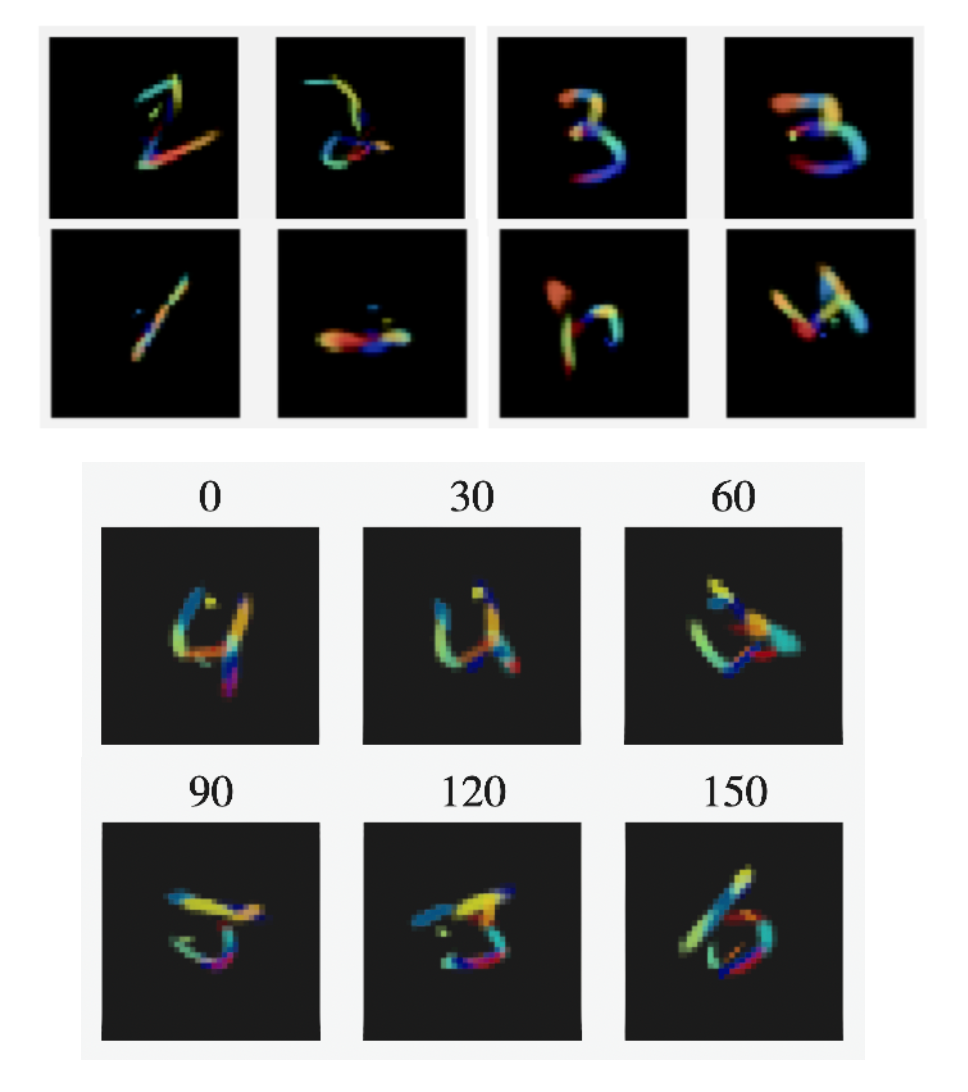
Reconstructions of the model, with the templates coloured in.
As before, we can see that the model uses the same templates for corresponding parts of images which are only translated by a small amount, but for images with large differences in orientation it uses different templates for different parts. 7
This, of course, breaks the assumption about how objects are composed that should lead to the representational advantage of capsules in the first place! We assumed that a transformed object would be represented as a set of transformed parts, but this assumption is not respected, as instead we represent a transformation of the object with different parts. This means that the rotated version of an image cannot be represented as a transformed version of the canonical orientation.
What is going wrong?
Before I address some of these issues, I want to quickly justify the fact that the experiments I’m discussing are in the ‘toy’ setting of datasets based on MNIST. Generally speaking, this is a very fair criticism - MNIST is an unrealistically easy dataset, and conclusions made on it often don’t transfer to other situations. Having said that, I think that this is not one of those cases. In particular, we are talking about a particular failure on MNIST. MNIST being a simple dataset is often a cause of cool-sounding methods that work on it failing to generalise, but surely the fact that it is easy mean that a demonstration of failure is even more worrying!
With this out of the way, I think there are a few possible causes of these issues. The first issues is identifiability. One obvious problem with the templates learned by this model is that lots of them are very similar to one another. This is potentially a reaction to the restriction that there can only be one of every kind of object present in the image - being less naive about this (for example, allowing repeated objects or allowing a certain number of objects ‘per receptive field’) might improve this issue. But we can see a manifestation of this issue in the coloured reconstructions of high rotation images - while the reconstructions are ‘wrong’ in the sense that they don’t use corresponding parts in the way that we want, they are not too bad in terms of the image likelihood - these are accurate reconstructions of the input images. This is an identifiability problem - there are many ways to reconstruct an image from templates. In principle, our model should assigns higher likelihood to the ‘equivariant’ way, but in practice, the higher level objects can only begin to learn after the low level objects have begun to reconstruct the images. The high level objects are unlikely to be able to learn anything useful if the low level templates are used in this way, as there are no geometrical patterns formed by the low level templates to discover.
The second possible problem is related, but is potentially even more fundamental. This is an issue related to whether the pose of objects can really be defined. For example, consider an object with internal degrees of symmetry, like a square or a circle. The square is of course invariant to rotations in the degree 4 discrete rotation group (\(R_4 = \{0,\frac{\pi}{2}, \pi, \frac{3\pi}{2}, 2\pi\}\)), and the circle is invariant to rotation in general. This is actually important, because an important unspoken assumption in the capsule story is that the pose of an object can be obtained and is unambiguous. In contrast, if the object in question has an internal symmetry, its pose is not neatly defined - for instance, it is only really possible to infer the pose of a square up to a transformation in \(R_4\). However, the current formulation of capsules enforces that we define the full pose of any objects, which can lead to problems when dealing with symmetrical templates, as shown in the figure below.
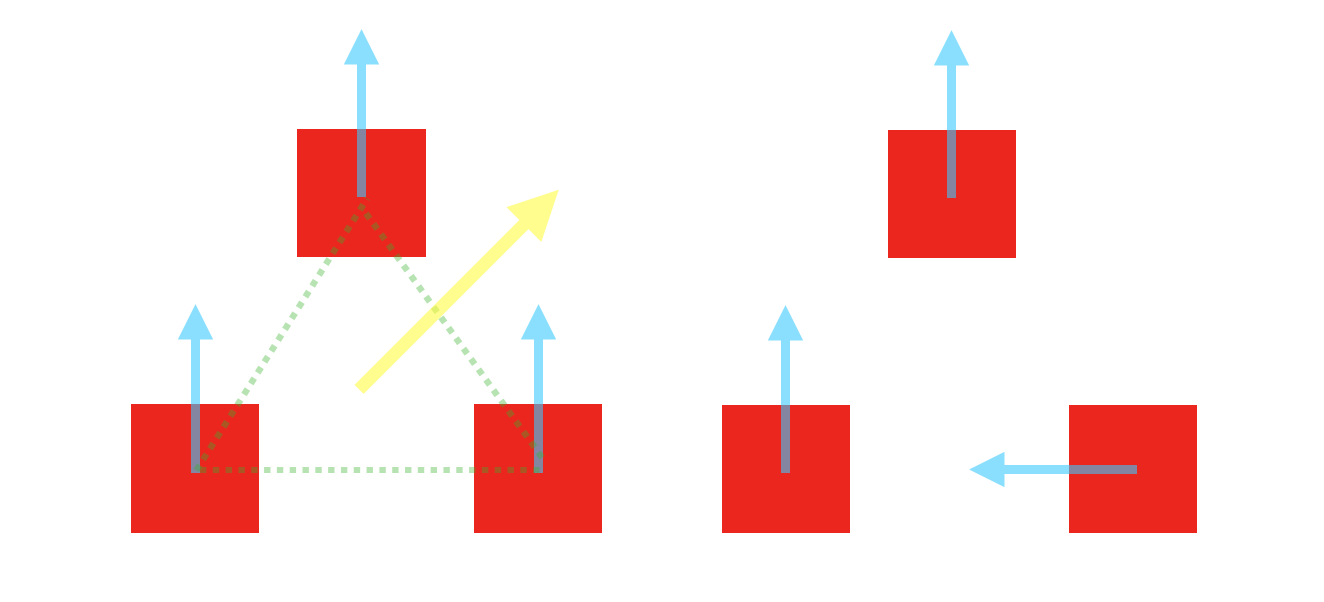
A cartoon illustrating what can go wrong if we don’t take into account the symmetry of objects. Consider a compound object (the green triangle) formed by three simple objects (the red squares). If we allow our capsule network to represent the full pose of objects, it must represent the full poses of the squares, as represented by the blue arrows, as well as the pose of the higher level object, represented by the yellow arrow. Due to the symmetry of the square, either one of these placements of the blue arrows is an identical reconstruction of the scene from the point of view of the low level objects, but since the high level object must predict the full poses of the constituent objects that make it up, it cannot represent both of these scenes with the same high level object, despite them being visually identical, since they differ in an ‘internal’ detail of the model.
It’s difficult to be sure if this is causing any problems, but I think it’s a conceptual issue that could be causing some problems, and I imagine that a solution which considered it carefully (e.g using group theory) would be likely to help other aspects of this kind of model as well.
What is an object, really?
Finally, there is a more ‘philosophical’ problem to the notion. Capsule papers, and more broadly, papers working on so called ‘object oriented’ approaches to machine learning, often talk as though it was obvious exactly what an ‘object’ is:
A capsule is a group of neurons whose activity vector represents the instantiation parameters of a specific type of entity such as an object or an object part (Sabour et. al.)
Objects are composed of a set of geometrically organised parts (Kosiorek et. al)
As the viewpoint changes, the pose matrices of the parts and the whole will change in a coordinated way (Hinton et. al.)
‘Capsule’ models try to explicitly represent the poses of objects (my own paper)
But of course, this is not necessarily obvious. The division of the world into objects, and the division of objects into constituent parts, is not an absolute property of reality, but a conceptual division which may be different in different contexts. At the risk of sounding pretentious, there is a quote I rather like from the Philosophical Investigations that puts this nicely
But what are the simple constituent parts of which reality is composed? – What are the simple constituent parts of a chair? – The pieces of wood from which it is assembled? Or the molecules, or the atoms? – “Simple” means: not composite. And here the point is: in what sense ‘composite’? It makes no sense at all to speak absolutely of the ‘simple parts of a chair’. Again: Does my visual image of this tree, of this chair, consist of parts? Multi-colouredness is one kind of compositeness; another is, for example, that of an open curve composed of straight bits. And a continuous curve may be said to be composed of an ascending and a descending segment. If I tell someone without any further explanation “What I see before me now is composite” he will legitimately ask “What do you mean by composite? For there are all sorts of things it may mean!” – The question “Is what you see composite?” makes good sense if it is already established what kind of compositeness – that is, which particular use of this word – is in question. (Wittgenstein, Philosophical Investigations, §47.)
The point Wittgenstein is making here is that whether something is an ‘object’ or not, or whether an object is simple or composite, is relative to our definition of ‘simple’, and there are a wide variety of meanings we might usefully assign to this. I touched on this point earlier when I talked about a bit about instantiation parameters; whether objects were considered the same depended on how we chose our transformations.
To walk through a practical example, the Chinese character 明 is a single word (meaning ‘bright’) but can be viewed as visually composed of the characters 日 and 月 (sun and moon). Similarly, we could think of the strokes making up these smaller characters as the fundamental ‘simple objects’ rather than the character set. This idea of geometrical arrangement can be somewhat difficult - to take the character 明 again, is this a ‘geometrical arrangement’ of the smaller objects 日 and 月, or a geometrical arrangement of lines? The answer to this question, insofar as it makes sense, is not a feature of any dataset of Chinese characters.
Rather, which of these we regard as ‘objects’ that we want to model the relations between is highly task dependent. If we are reading a Chinese text, then presumably we may regard 明 as a single word, the simplest constituent part of language. If we are taking a calligraphy class, then perhaps we will consider it as a composite collection of strokes that we need to draw in a particular way, with the strokes and their relations to each other being the fundamental objects of interest. If we are being taught how to read Chinese characters at a beginner level, perhaps we have already learned the characters 日 and 月, and viewing 明 as a composite object may be helpful in remembering how to draw or recognise it until we are familiar enough with it to recognise it as a simple word. The picture is complicated further by the presence in Mandarin of words consisting of multiple characters, like 明天 (tomorrow) - depending on the context, 明 may either be an ‘atomic’ word, or just part of the spelling of a larger word8. From the grammatical perspective, 明 and 明天 are the same ‘level’ of object, despite one being visually composite in terms of characters and the other not. Similarly, 明 and 天 are both characters, but 明 is (in one sense) a ‘composite’ character, with two recognisable components which are characters themselves, but 天 is not. It’s not my area of expertise, but it seems likely that someone reading text doesn’t perceive words because they subconsciously perceive arrangements of letters, as shown by the fact that mst rdrs r xtrmly tlrnt f mssng lttrs nd spllng mstks. The point is that even in a relatively simple task like character recognition - no one at a modern machine learning conference would be particularly impressed by a model which could perform character recognition on Chinese characters - imposing a division into ‘objects’ isn’t as simple as it might appear at first glance, even if we allow hierarchies of objects.
Of course, none of this scepticism is necessarily a reason to give up on object structured representations. That no decomposition of the world into objects is logically justified over another doesn’t necessarily mean that we can’t find a bias towards one particular decomposition which is helpful in a large variety of tasks that we actually care about. But in the process of designing models with these biases, we need to bear in mind how tricky the word ‘object’ can be, which is easy to forget when you spend too long working with example datasets like MNIST and CLEVR, where there is only a single concept of object that really makes sense to an observer.

An example image from the CLEVR dataset from Facebook research. In this context, what an object is seems very straightforward.
For capsules; the decomposition of objects into geometrically arranged parts is not always natural or straightforward, particularly if we are vague about what exactly those parts are. When we recognise words, do we do so by regarding them as collections of strokes? Letters? Characters? It is worth thinking about whether a capsule model could express that factually and fctlly should be recognised as the same word - I somewhat suspect that the generative model I outlined earlier could not, as given the pose of the overall word it would be required to make strong predictions for the positions of the letters - so f ct lly might be recognisable, but missing vowels which also involve a change of position might not be expressible by the generative model. While this may seem a bit downbeat, I think it actually shows a big advantage of thinking about our model in a generative way - with a clear generative model, this flaw is obvious, whereas it presumably still exists in capsule models which use a similar generative model implicitly to derive their routing algorithm, but is much less obvious.
So the conclusion I want to draw from this philosophical analysis is not that doing object oriented learning is pointless, but that we need to be aware of the vagueness of the term and think carefully about how our models are actually defining it, as opposed to the notion we want them to capture. Exactly what we want them to capture is likely to depend on the downstream task we are really interested in.
Conclusions
It’s always difficult to draw negative conclusions from empirical work. We can never quite be sure that with enough tweaking, this model couldn’t be made to work really well. But I am a bit sceptical of this, for reasons that I hope I’ve made clear in this post. I still think it was worth formulating this model - as I pointed out, some of these issues with the intuition only become apparent when you try to write down really carefully what exactly the model is that you are trying to perform inference in.
But I want to talk a bit about ways forward, rather than just flaws in a particular esoteric model. Have we learned anything in particular about how to organise this kind of model?
There are a few conclusions that I have personally taken from this stuff - your own may vary.
1. Thinking about poses requires thinking more carefully about group theory
There has been a reasonably rich literature on group theory and neural networks in the last few years. I personally didn’t take too much time to engage with it on a very deep level until recently, as the level of formalism in these papers can obscure their insights to those unfamiliar with group theory. However, I’m now more convinced that this formalism is worth the effort, and having experimented with it a fair amount I’m also extremely convinced that neural networks are unlikely to recover the kind of transformation equivariant mappings that capsule networks are aimed at without significant constraints on network design. For future work that goes down the generative route and tries to model pose, I think that thinking about the symmetry properties of objects is likely to be important, as objects with internal symmetry somewhat break the assumptions of capsules.
2. You need to know what you want to have objects for
I think that having object structured models, which is to say, models that have a capacity for compositional or relational representations of input in a broad sense, are a really interesting direction, and I hope to keep playing with them in the future. But having said that, I am not sure how much sense it makes to talk about object structured models in isolation from a task. Object is one of those elusive words that we are surrounded by when we try to talk about intelligence 9, that sound very intuitive but are extremely difficult to try to pin down. Now I don’t think that this problem is impossible, but I am increasingly sceptical about doing it unsupervised - which are the natural ‘objects’ can only really be defined in a particular context, as I tried to show with my example about the Chinese characters. If I just show you a symbol like 明天 and ask ‘where are the objects and parts’ there can’t really be a very sensible answer. If you have a particular task in mind, like reconstructing scenes or modelling dynamics, then there may be a representational advantage to had by adding structure to your model, but this is different because we have a benchmark to measure the usefulness of such structures against. There may be a form of ‘object bias’ which is broad and useful across a range of tasks, but there is no guarantee of it.
3. Image likelihoods are a big pain
This is a bit orthogonal to some of the deeper issues I talked about in this post, but I actually think that it’s a big problem for this kind of model. One of the ugliest parts of our setup - the template model - is necessary at least in part because of our requirement to specify a likelihood in the pixel space. This likelihood is often extremely unrealistic, and I think it’s a big reason these kinds of probabilistic models for images are less useful than we might hope - your principled Bayesian approach is often only as principled as its weakest link, and pixel likelihoods are pretty weak. There may be ways around this, but I haven’t thought of any so far. I think that exploring alternatives to pixel likelihoods for structured models like this, like GANs, bisimulation metrics and constrastive losses, is an important line of research which has been fairly promising lately.
Working with this kind of model has been pretty frustrating in many ways, but it’s also been extremely interesting, and I like to think that our model has been very revealing even if it hasn’t lead to any state of the art performance, or is likely to. I hope that this post has been useful or enlightening, at least to some readers, about the kind of ‘bigger picture’ problems that it’s worth thinking about and addressing when we are designing this kind of model. In particular, I’m very proud of our experimental evaluation on adding transformations to the training set for capsules, and would be very happy if I saw this kind of analysis replicated in new capsule papers!
If you have enjoyed this post and you are reading it before ICML 2020, then you can come and chat to me at the Object Oriented Learning Workshop about my workshop paper, and some of the topics here too if you like. If you are reading this afterwards, then feel free to get in touch via email.
Footnotes:
-
Interestingly, this means in this kind of model, object identity is also rate coded, as the models are invariant to permutation of the object slots. As we will see later, in capsule models object identity is still coded by place, i.e by having a particular neuron specialise to a particular kind of object. ↩
-
To be somewhat more ‘maths-y’ about this, consider that we have a set of elements \(X\), a group of transformations \(G\), and a binary relationship \(* : G \mapsto X \mapsto X\) defined between the elements of \(X\) and \(G\). We can define on \(X\) the equivalence relation \(\sim_G\), such that \(x \sim_G x'\Longleftrightarrow \exists g \in G : g * x' = x\). Calling two elements of \(x\) and \(x'\) ‘the same object’ in capsule terms is obviously more or less equivalent to a claim that \(x \sim_G x'\); that \(x\) can be represented as a transformation of \(x'\) and vice versa. But clearly we need a particular \(G\) to be attached to that tilde to be able to say anything about the equivalence of objects in this sense. If \(G\) is sufficiently powerful, then this becomes extremely uninteresting - if it is the set of all bijective functions, for instance, then we would conclude that all objects are equivalent. ↩
-
In fact, in a sense allowing very flexible transformations would bring us right back to normal neural network type models - a generative model like a VAE essentially treats all objects as ‘the same kind of’ object - all variation in the input images is modelled by a single vector of instantiation parameters, the latent variable, and there is no notion of having different objects except implicitly. ↩
-
We actually need to also include perspective projection in order to fully represent this, which we don’t do because it’s not currently implemented in Pytorch. But perspective projection is also a linear transformation so much of what I say still applies. ↩
-
In fact we want to avoid the zero matrix because it’s not really a member of our affine transformation group - we want to only consider affine transformations which are invertible, i.e have non-zero scale. Indeed, using this notation for Normal is lightly abusing notation - a more accurate description of what we do in the code is model the distribution over \(\mathrm{vec}(A-I)\). But saying \(\mathrm{Normal}(I, 1)\) gives you the idea. ↩
-
It may be possible to leverage group theory/steerable networks to design pose inference network which are much closer to being ‘correct by design’ - if models like this one are going to ‘work’ outside of toy settings, I think this is an obvious avenue to explore. ↩
-
In fact, qualitatively it seems like each template is pinned to a particular location, and the model changes template rather than translating the templates if they are translated by more than a small amount. This could potentially be an issue with the design of the encoder - at present it is a convnet which is equivariant to position, but as it predicts co-ordinates it may be important to add these to the image information, as in this paper. This is worth exploring, but I don’t believe that it’s the only issue with the model, as the identifiability problems I talk about later would remain. ↩
-
The characters ‘spell’ tomorrow in the sense that they tell you how to pronounce it; 明 is pronounced ‘míng’ and 天 (‘heaven’ or ‘sky’) is ‘tiān’, so tomorrow is ‘míngtiān’, but the meaning of the whole word doesn’t necessarily have anything to do with the meaning of the characters that make it up in isolation, though it’s often related. ↩
-
There is a whole other blog post of material here that I may get around to writing up one day… ↩
