Detecting hallucinations in large language models using semantic entropy

Sebastian Farquhar, Jannik Kossen, Lorenz Kuhn, Yarin Gal, 19 Jun 2024

Blog post accompanying Detecting Hallucinations in Large Language Models Using Semantic Entropy in Nature.

Large language models (LLMs) can do many things well. But their generations are often unreliable.

Sometimes this manifests as a lawyer using ChatGPT to look up legal precedents that are totally made up. Even more seriously, it could mean medical errors.

Ideally, there would be ways to start to tackle the “hallucination” problem for LLMs. In our recent paper in Nature, we make some progress.

What is hallucination?

The first step is to get a bit more precise. The word “hallucination” for LLMs has expanded to include almost every kind of being wrong. But there is no reason to expect that the same mechanism lies behind different ways to be wrong.

We focus on just one: confabulation. When an LLM confabulates, it makes something up for ‘no reason’. A key test is that it generates a different answer to the same prompt if you just ask the question again and sample with a different random seed.

Our experiments show that confabulation, in some sense the most straightforward kind of hallucination, is still a major component of LLM errors.

What does Semantic Uncertainty do?

We show how one can use uncertainty to detect confabulations. In principle, it seems plausible that a model that makes something up each time is uncertain about what the right answer is. A naive approach to estimating model uncertainty would just sample the outputs of a model multiple times and measure output variation as a way of measuring uncertainty. One example of this would be to compute the entropy of the outputs. This is high when lots of different responses are similarly likely, and low when there is just one response that the model is overwhelming likely to make.

This has been tried and doesn’t work that well.

The reason it doesn’t work well is because it doesn’t distinguish between cases where the LLM has lots of different ways to say the same thing, and cases where the LLM has lots of different things to say.

The first case can be what is called “lexical” or “syntactic” uncertainty - uncertainty about exactly which words to use.

The second can be called “semantic” uncertainty - uncertainty about the right meaning for the answer.

We introduce a family of methods for estimating semantic uncertainty. Specifically, we compute the “semantic entropy”, which is the entropy of the output distribution in “meaning-space” rather than “token-sequence-probability-space”.

Using our approach we can:

Identify which questions an LLM is likely to get wrong.
Refuse to answer questions that are likely to be answered wrong.
Get extra help when answering questions that are likely to be answered wrong.
Identify specific claims in longer passages which are likely to be wrong.

We show that this works across a range of models including GPT-4, LLaMA 2, and Falcon, with and without instruction tuning.

How it works

The method is simple to implement and you can copy our code. The key steps are:

Sample \(K\) answers. More \(K\) is better, but 5 or so is plenty.
Compute the token-sequence probability for each answer just by adding the log-probs of each chosen token (we normalize this by sequence length as well).
Check which answers mean the same thing as each other (the secret sauce - details below).
Add up the probabilities of answers that share a meaning.
Compute the entropy over these probabilities.

When that number is high, your question is likely to lead to wrong answers.

The key step is checking which answers mean the same thing as each other. This isn’t hard to do, it just takes an extra loop. We check if answers share a meaning in two ways. The easiest (but a bit more expensive) is to just ask a general-purpose LLM if they mean the same thing as each other. Another option is to use a cheaper dedicated Natural Language Inference model and see if each answer entails the other, which is often an indicator of a shared meaning.

There are some nuances here, that we go into in the paper. For example, context matters. In one case we found that the system treated “brain” and “central nervous system” as meaning the same thing, even though in the specific context of the question “Encephalytis is an inflamation of what?” they are different. If you want to use this in production, we strongly recommend checking some actual examples in your use case. But we generally found that the task of checking shared meaning is a lot easier for the LLM than answering the original question.

Then you can use a simple algorithm to add each new answer to one of the existing ‘meaning-clusters’ which you then add up the probabilities for. The full paper has some worked examples, and again you can just use our code.

How well does it work?

Pretty well. Across a range of question answering datasets, from natural questions to math to biology it helps determine cases where the answer is likely wrong.

We use two main metrics.

Area under the receiver operating characteristic curve (AUROC) represents how good the method is at predicting whether an answer is likely to be correct or incorrect.

Area under the rejection accuracy curve (AURAC) represents how much better your accuracy becomes if you reject (refuse to answer) the questions you are most uncertain about.

In both cases, 1 is the best score and higher is better. Our method has better scores than all baselines across a range of datasets and models.

We can also look in detail at some of the example generations and uncertainties as a way of getting a bit more intuition for what is going on.

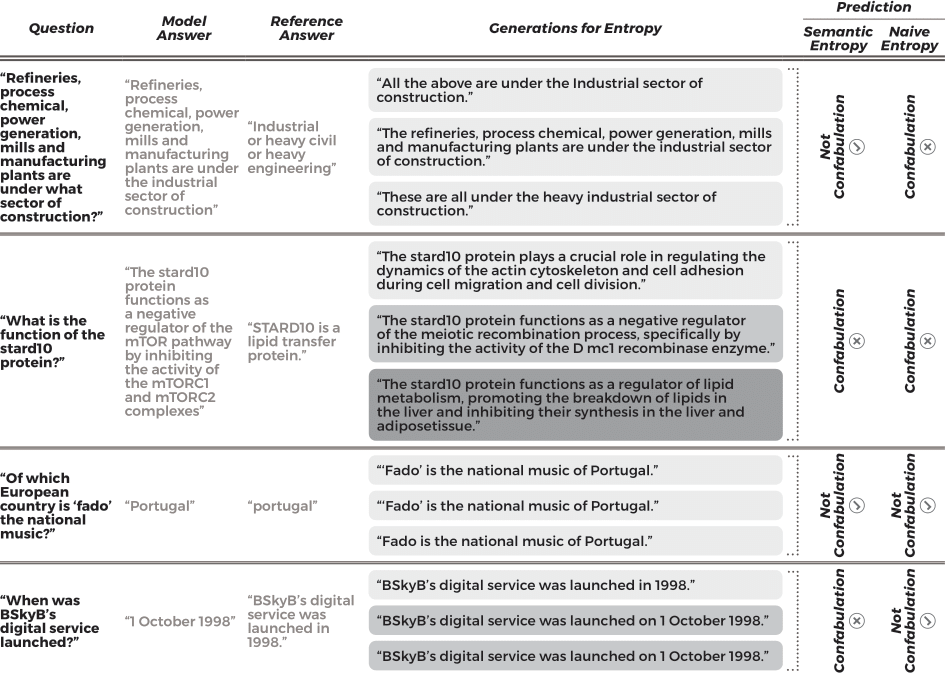
Table showing representative examples of generations from LLaMA 2 70B used for semantic entropy.

This table gives four kinds of examples, in the first one the generations from the model mean the same thing as each other so they are clustered together despite using different phrasings. For the second one, semantic entropy and naive entropy would both correctly predict a confabulation, because there is variation in both meaning and form. The third example is a case where semantic entropy and naive entropy would both correctly predict no confabulation because the multiple generations are almost lexically identical.

The fourth example shows one way semantic entropy can break. In our experiment, semantic entropy clustered the answers into those which provided a specific date and those which gave only a year, so the result was considered uncertain.

What does all this mean?

We think semantic entropy is a useful tool for cases where you need a bit more reliability from your LLM. In particular, if you use semantic entropy, you can be moderately confident that you can rule out a ‘careless error’ from your model. In many settings this is a big portion of the errors.

You shouldn’t over-rely on it though. Semantic entropy won’t catch:

Cases where the model has been trained into an incorrect style of reasoning or set of facts.
Cases where the model has been trained in a way that doesn’t apply to a new setting or context.
Cases where the model is engaging in ‘deliberate’ deception.

We think all of these involve different mechanisms and need different solutions.

There is also the issue of cost. Using semantic entropy is a bit more expensive that just doing raw question-answering. Getting LLM generations is actually very cheap, so the extra reliability you get will often be worth more than the extra pennies per query.

The extra cost comes from the fact that you need multiple answer samples (maybe 5? you can get away with fewer). But it also comes from the step where you compare answers to cluster them into meanings. The cost of comparisons scales poorly with \(K\), but for small \(K\) the actual number of comparisons needed in practice is not too far off linear (especially with some efficiencies we describe in the paper). In effect, therefore, computing semantic entropy requires something in the ballpark of 10x as much compute as a raw question-answer, which will often be comparable to something like using chain-of-thought in practice.

Key differences to our earlier paper

Some readers may have already read the paper “Semantic Uncertainty: Linguistic Invariances for Uncertainty Estimation in Natural Language Generation” published at ICLR. There are a few substantial differences in this paper.

The main methodological difference is that we switched from estimating semantic entropy as \(\frac{1}{N} \sum_{i=1}^{N} \log p_i\) becomes \(\frac{1}{\sum p_i}\sum_{i=1}^{N} p_i \log p_i.\) We found empirically that this gives much better results, though mathematically the estimator whould have the same expected value.

There were a number of other changes:

We introduce a scheme for applying semantic entropy to paragraph-length text by extracting specific claims, generating questions that might have caused those claims, and then generating answers to those questions.
We introduce an additional ‘discrete’ variant of semantic entropy that can be computed without access to token probabilities while still performing well.
We consider newer models (GPT-4, LLaMA 2, Falcon, Mistral) although publishing timelines are slow enough that there are now even newer models one would want to try.
We consider more data types, such as math and natural questions.
We consider longer generations, looking at entire sentences for even the short answers, where the LLMs in the first paper struggled at this scale.
For these longer generations, we introduced new ways of estimating entailment using general-purpose LLMs, clustering generations into semantic meaning using a ‘non-defeating’ entailment (see paper), and lastly, moved to automatically assessing model accuracy using LLMs rather than metrics based on substring matching.
We fixed subtle bugs in the implementation related to tokenizers that made our results in the ICLR paper much worse than they would have been otherwise.

OATML