Back to all publications...
On the Connection between Neural Processes and Gaussian Processes with Deep Kernels
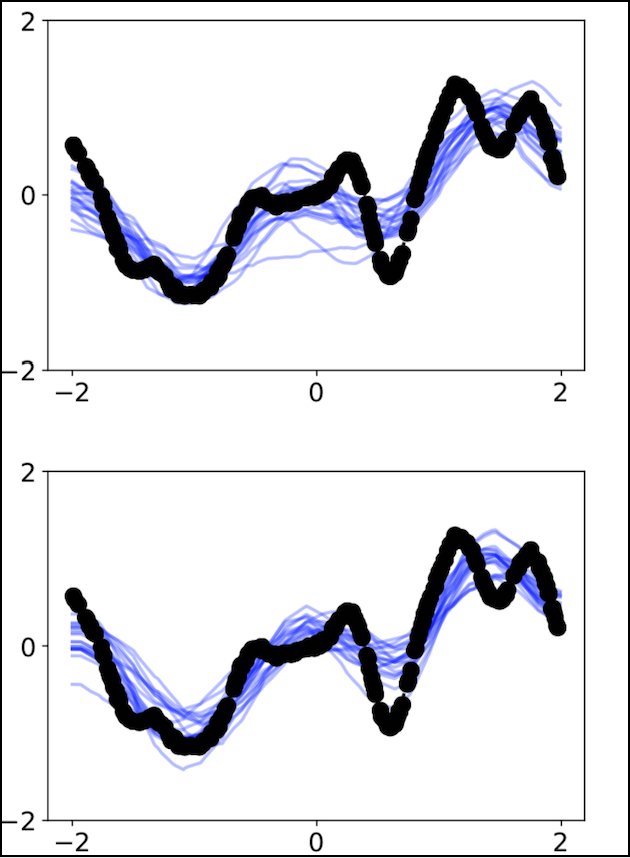
Neural Processes (NPs) are a class of neural latent variable models that combine desirable properties of Gaussian Processes (GPs) and neural networks. Like GPs, NPs define distributions over functions and are able to estimate the uncertainty in their predictions. Like neural networks, NPs are computationally efficient during training and prediction time. We establish a simple and explicit connection between NPs and GPs. In particular, we show that, under certain conditions, NPs are mathematically equivalent to GPs with deep kernels. This result further elucidates the relationship between GPs and NPs and makes previously derived theoretical insights about GPs applicable to NPs. Furthermore, it suggests a novel approach to learning expressive GP covariance functions applicable across different prediction tasks by training a deep kernel GP on a set of datasets
Tim G. J. Rudner, Vincent Fortuin, Yee Whye Teh, Yarin Gal
NeurIPS Workshop on Bayesian Deep Learning, 2018
[Paper] [BibTex]