Inference — Publications
Rethinking Aleatoric and Epistemic Uncertainty
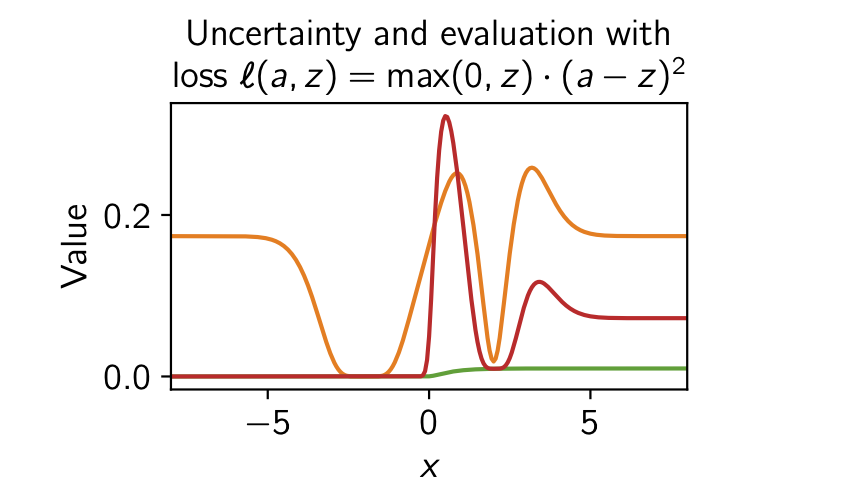
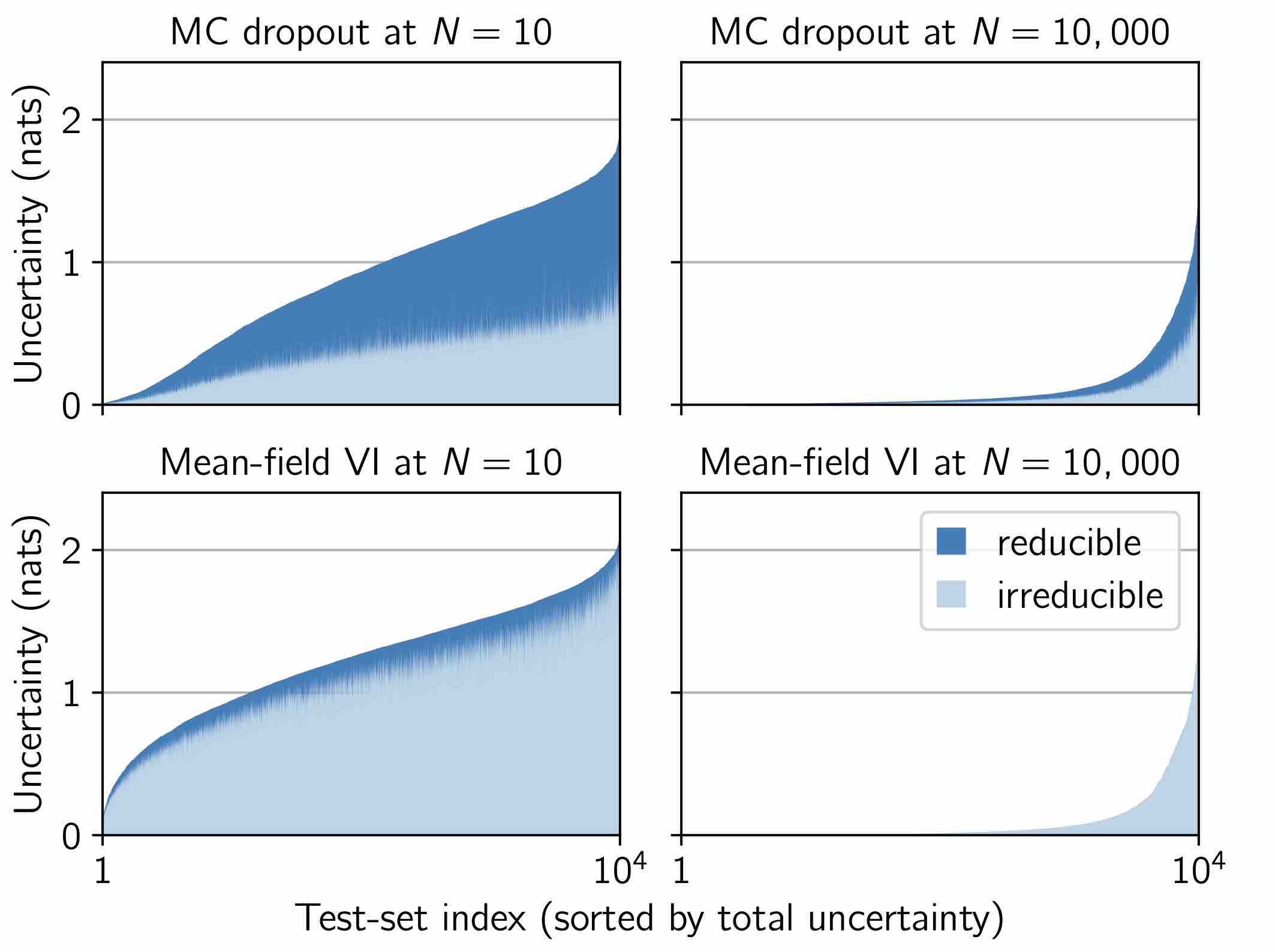
The ideas of aleatoric and epistemic uncertainty are widely used to reason about the probabilistic predictions of machine-learning models. We identify incoherence in existing discussions of these ideas and suggest this stems from the aleatoric-epistemic view being insufficiently expressive to capture all the distinct quantities that researchers are interested in. To address this we present a decision-theoretic perspective that relates rigorous notions of uncertainty, predictive performance and statistical dispersion in data. This serves to support clearer thinking as the field moves forward. Additionally we provide insights into popular information-theoretic quantities, showing they can be poor estimators of what they are often purported to measure, while also explaining how they can still be useful in guiding data acquisition.
Freddie Bickford Smith, Jannik Kossen, Eleanor Trollope, Mark van der Wilk, Adam Foster, Tom Rainforth
International Conference on Machine Learning (ICML), 2025
[Paper] [BibTeX]
Temporal-Difference Variational Continual Learning
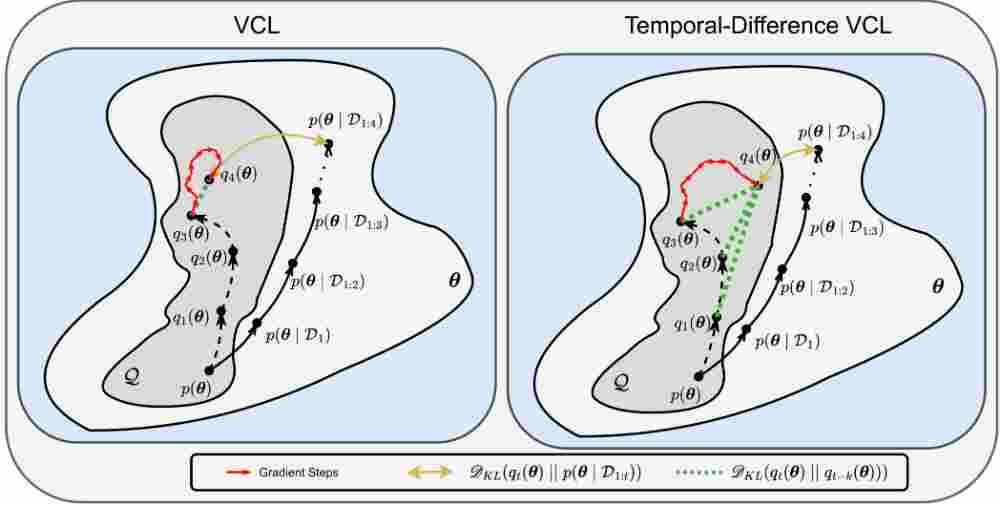
A crucial capability of Machine Learning models in real-world applications is the ability to continuously learn new tasks. This adaptability allows them to respond to potentially inevitable shifts in the data-generating distribution over time. However, in Continual Learning (CL) settings, models often struggle to balance learning new tasks (plasticity) with retaining previous knowledge (memory stability). Consequently, they are susceptible to Catastrophic Forgetting, which degrades performance and undermines the reliability of deployed systems. Variational Continual Learning methods tackle this challenge by employing a learning objective that recursively updates the posterior distribution and enforces it to stay close to the latest posterior estimate. Nonetheless, we argue that these methods may be ineffective due to compounding approximation errors over successive recursions. To mitigate this, we propose new learning objectives that integrate the regularization effects of multi... [full abstract]
Luckeciano Carvalho Melo, Alessandro Abate, Yarin Gal
arXiv
[paper]
Making Better Use of Unlabelled Data in Bayesian Active Learning
Fully supervised models are predominant in Bayesian active learning. We argue that their neglect of the information present in unlabelled data harms not just predictive performance but also decisions about what data to acquire. Our proposed solution is a simple framework for semi-supervised Bayesian active learning. We find it produces better-performing models than either conventional Bayesian active learning or semi-supervised learning with randomly acquired data. It is also easier to scale up than the conventional approach. As well as supporting a shift towards semi-supervised models, our findings highlight the importance of studying models and acquisition methods in conjunction.
Freddie Bickford Smith, Adam Foster, Tom Rainforth
International Conference on Artificial Intelligence and Statistics (AISTATS), 2024
[Paper] [BibTeX]
Modern Bayesian Experimental Design
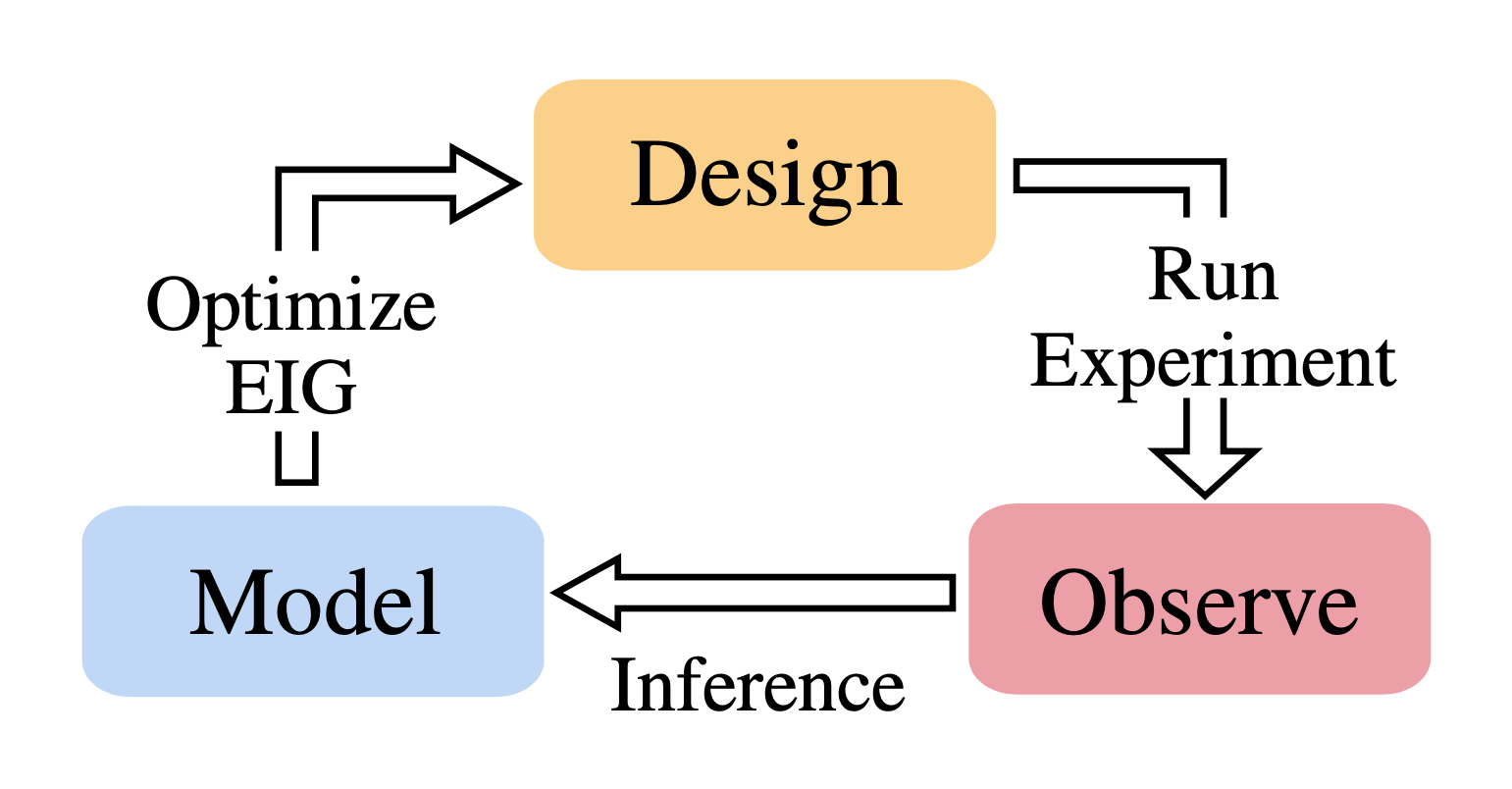
Bayesian experimental design (BED) provides a powerful and general framework for optimizing the design of experiments. However, its deployment often poses substantial computational challenges that can undermine its practical use. In this review, we outline how recent advances have transformed our ability to overcome these challenges and thus utilize BED effectively, before discussing some key areas for future development in the field.
Tom Rainforth, Adam Foster, Desi R. Ivanova, Freddie Bickford Smith
Statistical Science
[Paper] [BibTeX]
Drug Discovery under Covariate Shift with Domain-Informed Prior Distributions over Functions
Accelerating the discovery of novel and more effective therapeutics is a major pharmaceutical problem in which deep learning plays an increasingly important role. However, drug discovery tasks are often characterized by a scarcity of labeled data and significant covariate shift—settings that are challenging for standard deep learning methods. In this paper, we address this challenge by developing a probabilistic model that is able to encode prior knowledge about the data-generating process into a prior distribution over functions, allowing researchers to explicitly specify relevant information about the modeled domain. We evaluate this method on a novel, high-quality antimalarial dataset that facilitates the robust comparison of models in an extrapolative regime and demonstrate that integrating explicit prior knowledge of drug-like chemical space into the modeling process substantially improves both the predictive accuracy and the uncertainty estimates of deep learning algorithm... [full abstract]
Leo Klarner, Tim G. J. Rudner, Michael Reutlinger, Torsten Schindler, Garrett M Morris, Charlotte Deane, Yee Whye Teh
ICML, 2023
[OpenReview] [BibTex]
Can Active Sampling Reduce Causal Confusion in Offline Reinforcement Learning?
Causal confusion is a phenomenon where an agent learns a policy that reflects imperfect spurious correlations in the data. Such a policy may falsely appear to be optimal during training if most of the training data contain such spurious correlations. This phenomenon is particularly pronounced in domains such as robotics, with potentially large gaps between the open- and closed-loop performance of an agent. In such settings, causally confused models may appear to perform well according to open-loop metrics during training but fail catastrophically when deployed in the real world. In this paper, we study causal confusion in offline reinforcement learning. We investigate whether selectively sampling appropriate points from a dataset of demonstrations may enable offline reinforcement learning agents to disambiguate the underlying causal mechanisms of the environment, alleviate causal confusion in offline reinforcement learning, and produce a safer model for deployment. To answer thi... [full abstract]
Gunshi Gupta, Tim G. J. Rudner, Rowan McAllister, Adrien Gaidon, Yarin Gal
CLeaR, 2023
NeurIPS Workshop on Causal Machine Learning for Real-World Impact, 2022
[OpenReview] [BibTex]
Prediction-Oriented Bayesian Active Learning
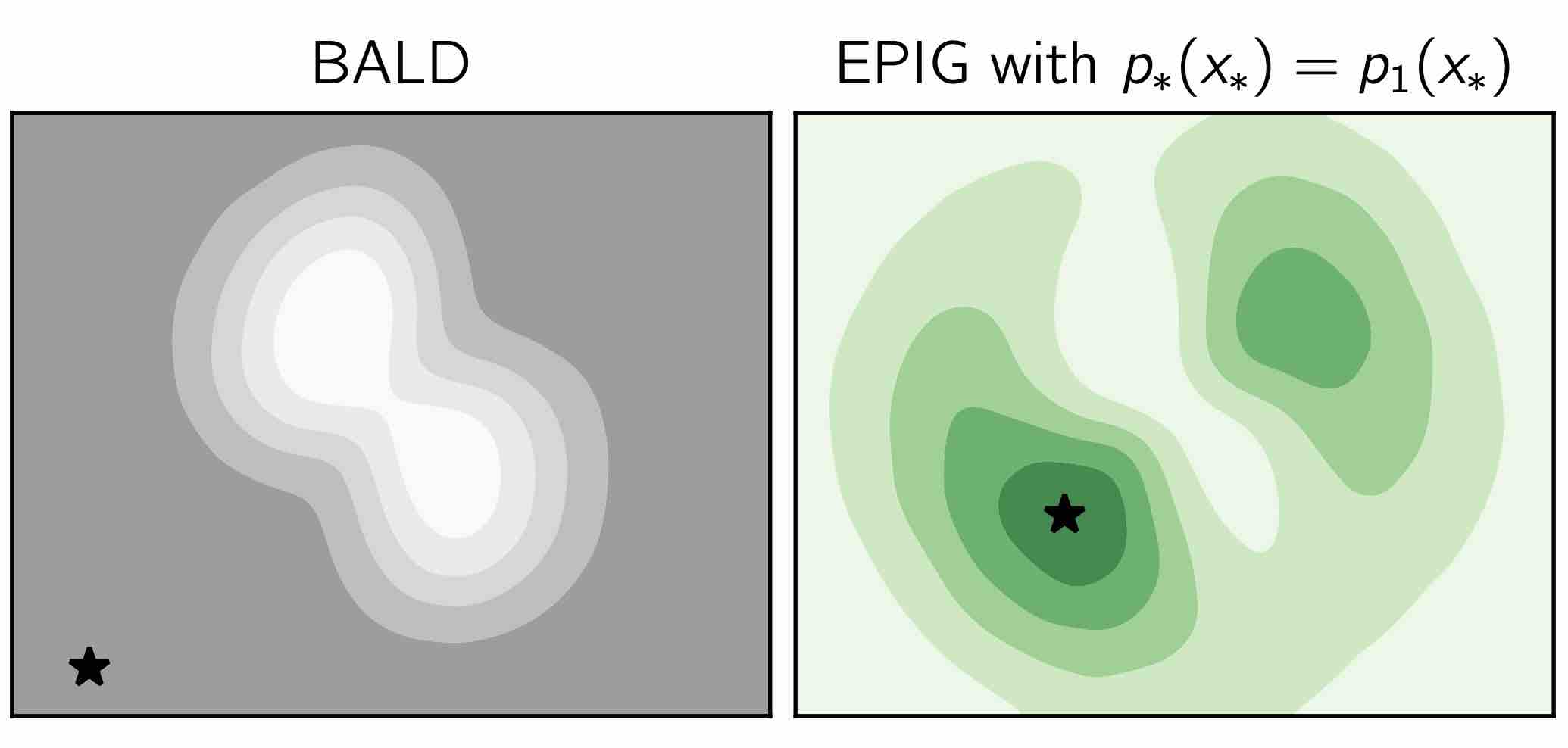
Information-theoretic approaches to active learning have traditionally focused on maximising the information gathered about the model parameters, most commonly by optimising the BALD score. We highlight that this can be suboptimal from the perspective of predictive performance. For example, BALD lacks a notion of an input distribution and so is prone to prioritise data of limited relevance. To address this we propose the expected predictive information gain (EPIG), an acquisition function that measures information gain in the space of predictions rather than parameters. We find that using EPIG leads to stronger predictive performance compared with BALD across a range of datasets and models, and thus provides an appealing drop-in replacement.
Freddie Bickford Smith, Andreas Kirsch, Sebastian Farquhar, Yarin Gal, Adam Foster, Tom Rainforth
International Conference on Artificial Intelligence and Statistics (AISTATS), 2023
[Paper] [BibTeX]
Tractable Function-Space Variational Inference in Bayesian Neural Networks
Reliable predictive uncertainty estimation plays an important role in enabling the deployment of neural networks to safety-critical settings. A popular approach for estimating the predictive uncertainty of neural networks is to define a prior distribution over the network parameters, infer an approximate posterior distribution, and use it to make stochastic predictions. However, explicit inference over neural network parameters makes it difficult to incorporate meaningful prior information about the data-generating process into the model. In this paper, we pursue an alternative approach. Recognizing that the primary object of interest in most settings is the distribution over functions induced by the posterior distribution over neural network parameters, we frame Bayesian inference in neural networks explicitly as inferring a posterior distribution over functions and propose a scalable function-space variational inference method that allows incorporating prior information and re... [full abstract]
Tim G. J. Rudner, Zonghao Chen, Yee Whye Teh, Yarin Gal
NeurIPS, 2022
ICML Workshop on Uncertainty & Robustness in Deep Learning, 2021
[OpenReview] [BibTex]
Plex: Towards Reliability using Pretrained Large Model Extensions
A recent trend in artificial intelligence is the use of pretrained models for language and vision tasks, which have achieved extraordinary performance but also puzzling failures. Probing these models’ abilities in diverse ways is therefore critical to the field. In this paper, we explore the reliability of models, where we define a reliable model as one that not only achieves strong predictive performance but also performs well consistently over many decision-making tasks involving uncertainty (e.g., selective prediction, open set recognition), robust generalization (e.g., accuracy and proper scoring rules such as log-likelihood on in- and out-of-distribution datasets), and adaptation (e.g., active learning, few-shot uncertainty). We devise 10 types of tasks over 40 datasets in order to evaluate different aspects of reliability on both vision and language domains. To improve reliability, we developed ViT-Plex and T5-Plex, pretrained large model extensions for vision and language... [full abstract]
Dustin Tran, Jeremiah Liu, Michael W. Dusenberry, Du Phan, Mark Collier, Jie Ren, Kehang Han, Zi Wang, Zelda Mariet, Huiyi Hu, Neil Band, Tim G. J. Rudner, Karan Singhal, Zachary Nado, Joost van Amersfoort, Andreas Kirsch, Rodolphe Jenatton, Nithum Thain, Honglin Yuan, Kelly Buchanan, Kevin Murphy, D. Sculley, Yarin Gal, Zoubin Ghahramani, Jasper Snoek, Balaji Lakshminarayan
Contributed Talk, ICML Pre-training Workshop, 2022
[OpenReview] [Code] [BibTex] [Google AI Blog Post]
Continual Learning via Sequential Function-Space Variational Inference
Sequential Bayesian inference over predictive functions is a natural framework for continual learning from streams of data. However, applying it to neural networks has proved challenging in practice. Addressing the drawbacks of existing techniques, we propose an optimization objective derived by formulating continual learning as sequential function-space variational inference. In contrast to existing methods that regularize neural network parameters directly, this objective allows parameters to vary widely during training, enabling better adaptation to new tasks. Compared to objectives that directly regularize neural network predictions, the proposed objective allows for more flexible variational distributions and more effective regularization. We demonstrate that, across a range of task sequences, neural networks trained via sequential function-space variational inference achieve better predictive accuracy than networks trained with related methods while depending less on maint... [full abstract]
Tim G. J. Rudner, Freddie Bickford Smith, Qixuan Feng, Yee Whye Teh, Yarin Gal
ICML, 2022
ICML Workshop on Theory and Foundations of Continual Learning, 2021
[Paper] [BibTex]
Challenges and Opportunities in Offline Reinforcement Learning from Visual Observations
Offline reinforcement learning has shown great promise in leveraging large pre-collected datasets for policy learning, allowing agents to forgo often-expensive online data collection. However, to date, offline reinforcement learning from visual observations with continuous action spaces has been relatively under-explored, and there is a lack of understanding of where the remaining challenges lie. In this paper, we seek to establish simple baselines for continuous control in the visual domain. We show that simple modifications to two state-of-the-art vision-based online reinforcement learning algorithms, DreamerV2 and DrQ-v2, suffice to outperform prior work and establish a competitive baseline. We rigorously evaluate these algorithms on both existing offline datasets and a new testbed for offline reinforcement learning from visual observations that better represents the data distributions present in real-world offline RL problems, and open-source our code and data to facilitate ... [full abstract]
Cong Lu, Philip J. Ball, Tim G. J. Rudner, Jack Parker-Holder, Michael A. Osborne, Yee Whye Teh
Outstanding Paper Award, RSS Workshop on Learning from Diverse, Offline Data, 2022
ICML Workshop on Decision Awareness in Reinforcement Learning, 2022
[arXiv] [BibTex]
On Pathologies in KL-Regularized Reinforcement Learning from Expert Demonstrations
KL-regularized reinforcement learning from expert demonstrations has proved successful in improving the sample efficiency of deep reinforcement learning algorithms, allowing them to be applied to challenging physical real-world tasks. However, we show that KL-regularized reinforcement learning with behavioral policies derived from expert demonstrations suffers from hitherto unrecognized pathological behavior that can lead to slow, unstable, and suboptimal online training. We show empirically that the pathology occurs for commonly chosen behavioral policy classes and demonstrate its impact on sample efficiency and online policy performance. Finally, we show that the pathology can be remedied by specifying non-parametric behavioral policies and that doing so allows KL-regularized RL to significantly outperform state-of-the-art approaches on a variety of challenging locomotion and dexterous hand manipulation tasks.
Tim G. J. Rudner, Cong Lu, Michael A. Osborne, Yarin Gal, Yee Whye Teh
NeurIPS, 2021
ICLR Workshop on Robust and Reliable Machine Learning in the Real World, 2021
[OpenReview] [Website] [BibTex]
Outcome-Driven Reinforcement Learning via Variational Inference
While reinforcement learning algorithms provide automated acquisition of optimal policies, practical application of such methods requires a number of design decisions, such as manually designing reward functions that not only define the task, but also provide sufficient shaping to accomplish it. In this paper, we view reinforcement learning as inferring policies that achieve desired outcomes, rather than as a problem of maximizing rewards. To solve this inference problem, we establish a novel variational inference formulation that allows us to derive a well-shaped reward function which can be learned directly from environment interactions. From the corresponding variational objective, we also derive a new probabilistic Bellman backup operator and use it to develop an off-policy algorithm to solve goal-directed tasks. We empirically demonstrate that this method eliminates the need to hand-craft reward functions for a suite of diverse manipulation and locomotion tasks and leads to... [full abstract]
Tim G. J. Rudner, Vitchyr H. Pong, Rowan McAllister, Yarin Gal, Sergey Levine
NeurIPS, 2021
NeurIPS Workshop on Deep Reinforcement Learning, 2020
[arXiv] [OpenReview] [BibTex]
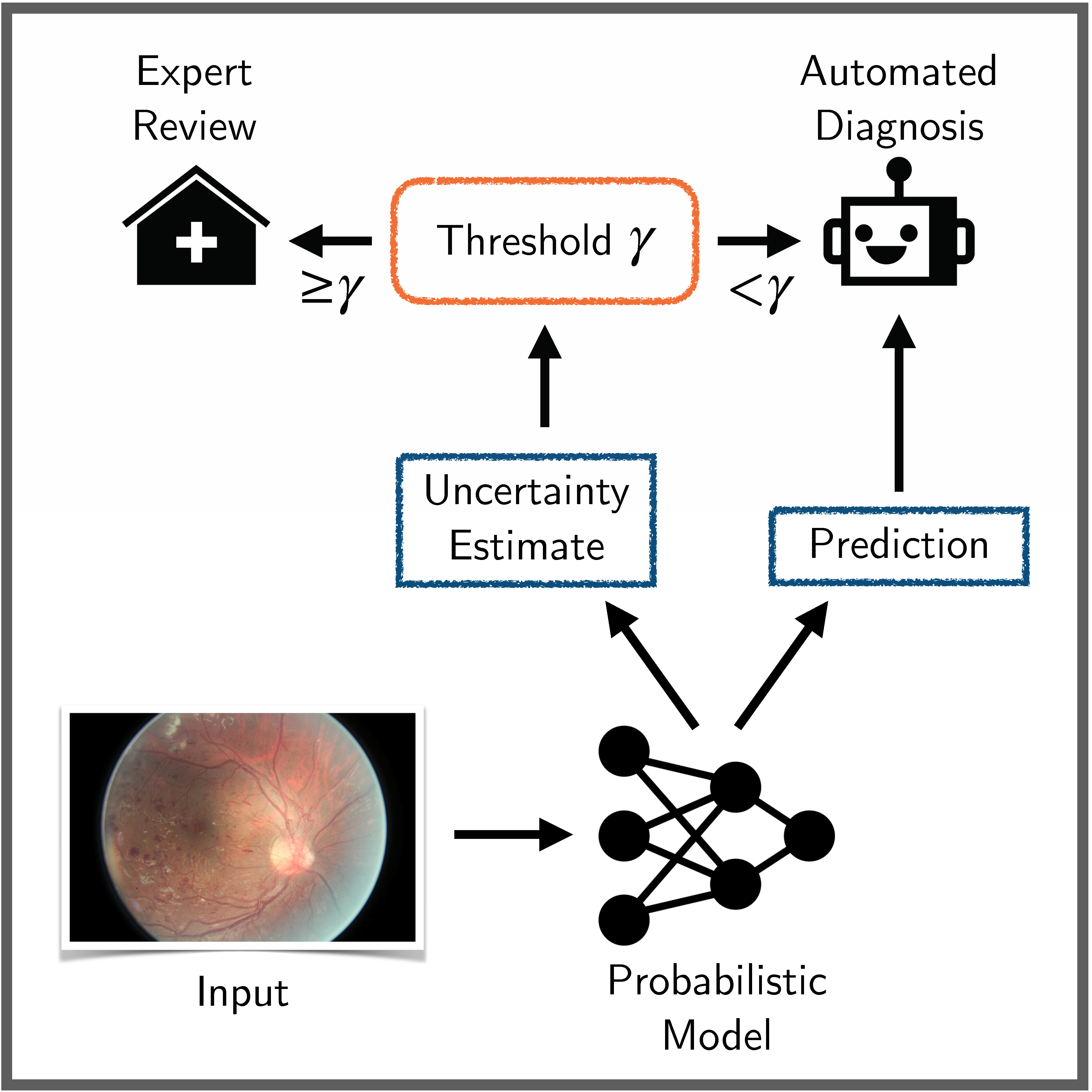
Benchmarking Bayesian Deep Learning on Diabetic Retinopathy Detection Tasks
Bayesian deep learning seeks to equip deep neural networks with the ability to precisely quantify their predictive uncertainty, and has promised to make deep learning more reliable for safety-critical real-world applications. Yet, existing Bayesian deep learning methods fall short of this promise; new methods continue to be evaluated on unrealistic test beds that do not reflect the complexities of downstream real-world tasks that would benefit most from reliable uncertainty quantification. We propose a set of real-world tasks that accurately reflect such complexities and are designed to assess the reliability of predictive models in safety-critical scenarios. Specifically, we curate two publicly available datasets of high-resolution human retina images exhibiting varying degrees of diabetic retinopathy, a medical condition that can lead to blindness, and use them to design a suite of automated diagnosis tasks that require reliable predictive uncertainty quantification. We use th... [full abstract]
Neil Band, Tim G. J. Rudner, Qixuan Feng, Angelos Filos, Zachary Nado, Michael W. Dusenberry, Ghassen Jerfel, Dustin Tran, Yarin Gal
NeurIPS Datasets and Benchmarks Track, 2021
Spotlight Talk, NeurIPS Workshop on Distribution Shifts, 2021
Symposium on Machine Learning for Health (ML4H) Extended Abstract Track, 2021
NeurIPS Workshop on Bayesian Deep Learning, 2021
[OpenReview] [Code] [BibTex]
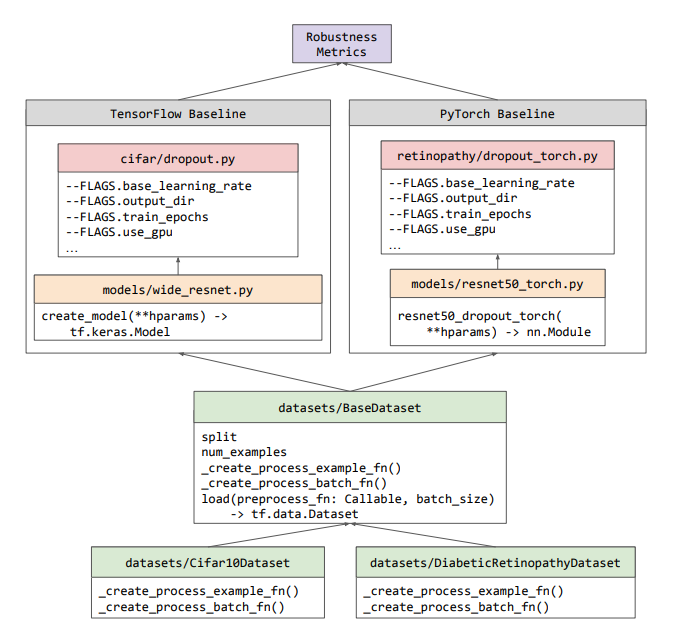
Uncertainty Baselines: Benchmarks for Uncertainty & Robustness in Deep Learning
High-quality estimates of uncertainty and robustness are crucial for numerous real-world applications, especially for deep learning which underlies many deployed ML systems. The ability to compare techniques for improving these estimates is therefore very important for research and practice alike. Yet, competitive comparisons of methods are often lacking due to a range of reasons, including: compute availability for extensive tuning, incorporation of sufficiently many baselines, and concrete documentation for reproducibility. In this paper we introduce Uncertainty Baselines: high-quality implementations of standard and state-of-the-art deep learning methods on a variety of tasks. As of this writing, the collection spans 19 methods across 9 tasks, each with at least 5 metrics. Each baseline is a self-contained experiment pipeline with easily reusable and extendable components. Our goal is to provide immediate starting points for experimentation with new methods or applications. A... [full abstract]
Zachary Nado, Neil Band, Mark Collier, Josip Djolonga, Michael W. Dusenberry, Sebastian Farquhar, Angelos Filos, Marton Havasi, Rodolphe Jenatton, Ghassen Jerfel, Jeremiah Liu, Zelda Mariet, Jeremy Nixon, Shreyas Padhy, Jie Ren, Tim G. J. Rudner, Yeming Wen, Florian Wenzel, Kevin Murphy, D. Sculley, Balaji Lakshminarayanan, Jasper Snoek, Yarin Gal, Dustin Tran
NeurIPS Workshop on Bayesian Deep Learning, 2021
[arXiv] [Code] [Blog Post (Google AI)] [BibTex]
Shifts: A Dataset of Real Distributional Shift Across Multiple Large-Scale Tasks
There has been significant research done on developing methods for improving robustness to distributional shift and uncertainty estimation. In contrast, only limited work has examined developing standard datasets and benchmarks for assessing these approaches. Additionally, most work on uncertainty estimation and robustness has developed new techniques based on small-scale regression or image classification tasks. However, many tasks of practical interest have different modalities, such as tabular data, audio, text, or sensor data, which offer significant challenges involving regression and discrete or continuous structured prediction. Thus, given the current state of the field, a standardized large-scale dataset of tasks across a range of modalities affected by distributional shifts is necessary. This will enable researchers to meaningfully evaluate the plethora of recently developed uncertainty quantification methods, as well as assessment criteria and state-of-the-art baselin... [full abstract]
Andrey Malinin, Neil Band, Alexander Ganshin, German Chesnokov, Yarin Gal, Mark J. F. Gales, Alexey Noskov, Andrey Ploskonosov, Liudmila Prokhorenkova, Ivan Provilkov, Vatsal Raina, Vyas Raina, Denis Roginskiy, Mariya Shmatova, Panagiotis Tigas, Boris Yangel
NeurIPS Datasets and Benchmarks Track, 2021
[arXiv] [BibTex] [Code]
[Competition Website] [Blog Post (OATML)] [Blog Post (Yandex Research)]
Provable Guarantees on the Robustness of Decision Rules to Causal Interventions
Robustness of decision rules to shifts in the data-generating process is crucial to the successful deployment of decision-making systems. Such shifts can be viewed as interventions on a causal graph, which capture (possibly hypothetical) changes in the data-generating process, whether due to natural reasons or by the action of an adversary. We consider causal Bayesian networks and formally define the interventional robustness problem, a novel model-based notion of robustness for decision functions that measures worst-case performance with respect to a set of interventions that denote changes to parameters and/or causal influences. By relying on a tractable representation of Bayesian networks as arithmetic circuits, we provide efficient algorithms for computing guaranteed upper and lower bounds on the interventional robustness probabilities. Experimental results demonstrate that the methods yield useful and interpretable bounds for a range of practical networks, paving the way to... [full abstract]
Benjie Wang, Clare Lyle, Marta Kwiatkowska
IJCAI, 2021
[Paper]
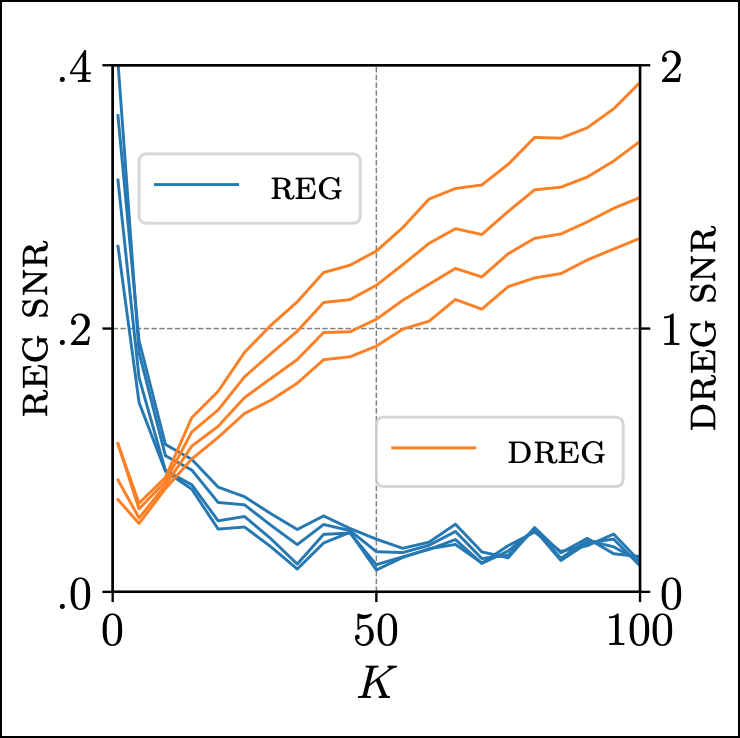
On Signal-to-Noise Ratio Issues in Variational Inference for Deep Gaussian Processes
We show that the gradient estimates used in training Deep Gaussian Processes (DGPs) with importance-weighted variational inference are susceptible to signal-to-noise ratio (SNR) issues. Specifically, we show both theoretically and empirically that the SNR of the gradient estimates for the latent variable’s variational parameters decreases as the number of importance samples increases. As a result, these gradient estimates degrade to pure noise if the number of importance samples is too large. To address this pathology, we show how doubly-reparameterized gradient estimators, originally proposed for training variational autoencoders, can be adapted to the DGP setting and that the resultant estimators completely remedy the SNR issue, thereby providing more reliable training. Finally, we demonstrate that our fix can lead to improvements in the predictive performance of the model’s predictive posterior.
Tim G. J. Rudner, Oscar Key, Yarin Gal, Tom Rainforth
ICML, 2021
[arXiv] [Code] [BibTex]
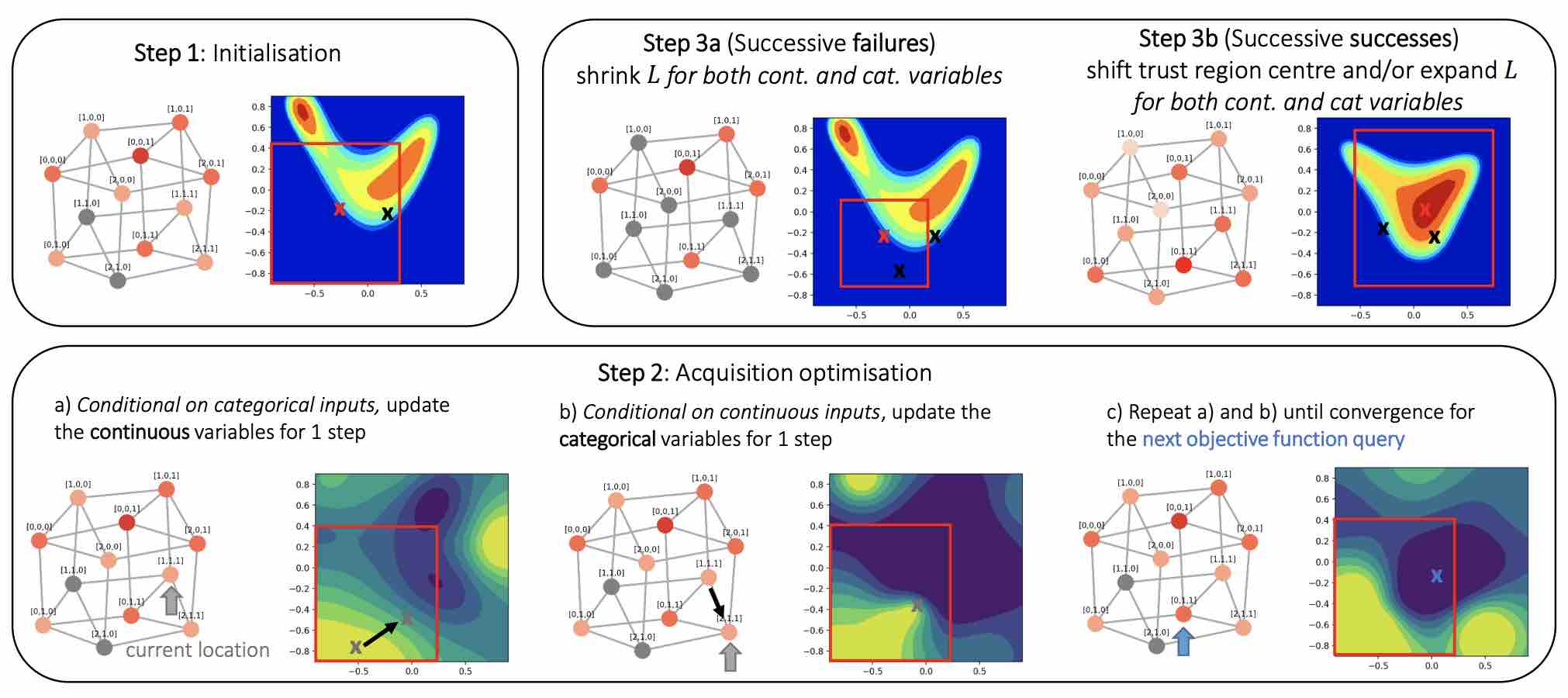
Think Global and Act Local: Bayesian Optimisation over High-Dimensional Categorical and Mixed Search Spaces
High-dimensional black-box optimisation remains an important yet notoriously challenging problem. Despite the success of Bayesian optimisation methods on continuous domains, domains that are categorical, or that mix continuous and categorical variables, remain challenging. We propose a novel solution – we combine local optimisation with a tailored kernel design, effectively handling highdimensional categorical and mixed search spaces, whilst retaining sample efficiency. We further derive convergence guarantee for the proposed approach. Finally, we demonstrate empirically that our method outperforms the current baselines on a variety of synthetic and real-world tasks in terms of performance, computational costs, or both.
Xingchen Wan, Vu Nguyen, Huong Ha, Binxin (Robin) Ru, Cong Lu, Michael A. Osborne
ICML, 2021
[Paper]
Active Testing: Sample-Efficient Model Evaluation
We introduce active testing: a new framework for sample-efficient model evaluation. While approaches like active learning reduce the number of labels needed for model training, existing literature largely ignores the cost of labeling test data, typically unrealistically assuming large test sets for model evaluation. This creates a disconnect to real applications where test labels are important and just as expensive, e.g. for optimizing hyperparameters. Active testing addresses this by carefully selecting the test points to label, ensuring model evaluation is sample-efficient. To this end, we derive theoretically-grounded and intuitive acquisition strategies that are specifically tailored to the goals of active testing, noting these are distinct to those of active learning. Actively selecting labels introduces a bias; we show how to remove that bias while reducing the variance of the estimator at the same time. Active testing is easy to implement, effective, and can be applied to... [full abstract]
Jannik Kossen, Sebastian Farquhar, Yarin Gal, Tom Rainforth
ICML, 2021
[PMLR] [arXiv]
Probabilistic Programs with Stochastic Conditioning
We tackle the problem of conditioning probabilistic programs on distributions of observable variables. Probabilistic programs are usually conditioned on samples from the joint data distribution, which we refer to as deterministic conditioning. However, in many real-life scenarios, the observations are given as marginal distributions, summary statistics, or samplers. Conventional probabilistic programming systems lack adequate means for modeling and inference in such scenarios. We propose a generalization of deterministic conditioning to stochastic conditioning, that is, conditioning on the marginal distribution of a variable taking a particular form. To this end, we first define the formal notion of stochastic conditioning and discuss its key properties. We then show how to perform inference in the presence of stochastic conditioning. We demonstrate potential usage of stochastic conditioning on several case studies which involve various kinds of stochastic conditioning and are d... [full abstract]
David Tolpin, Yuan Zhou, Tom Rainforth, Hongseok Yang
ICML, 2021
[arXiv]
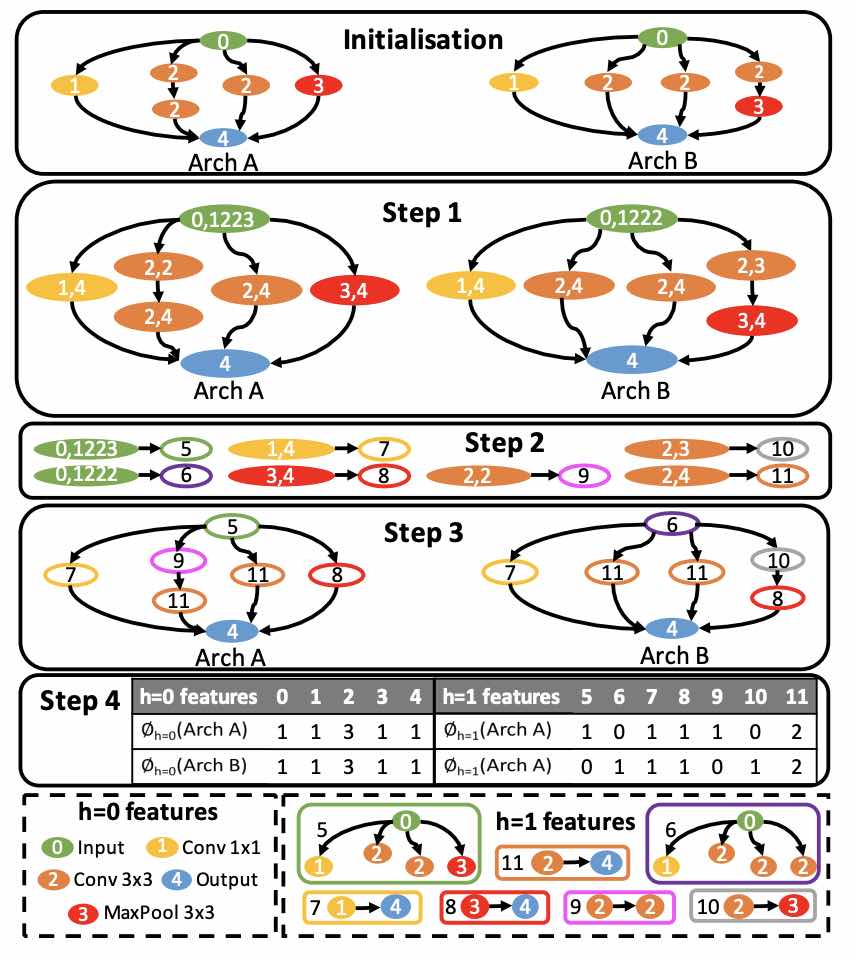
Interpretable Neural Architecture Search via Bayesian Optimisation with Weisfeiler-Lehman Kernels
Current neural architecture search (NAS) strategies focus only on finding a single, good, architecture. They offer little insight into why a specific network is performing well, or how we should modify the architecture if we want further improvements. We propose a Bayesian optimisation (BO) approach for NAS that combines the Weisfeiler-Lehman graph kernel with a Gaussian process surrogate. Our method not only optimises the architecture in a highly data-efficient manner, but also affords interpretability by discovering useful network features and their corresponding impact on the network performance. Moreover, our method is capable of capturing the topological structures of the architectures and is scalable to large graphs, thus making the high-dimensional and graph-like search spaces amenable to BO. We demonstrate empirically that our surrogate model is capable of identifying useful motifs which can guide the generation of new architectures. We finally show that our method outpe... [full abstract]
Binxin (Robin) Ru, Xingchen Wan, Xiaowen Dong, Michael A. Osborne
ICLR, 2021
[Paper]
On Statistical Bias In Active Learning: How and When to Fix It
Active learning is a powerful tool when labelling data is expensive, but it introduces a bias because the training data no longer follows the population distribution. We formalize this bias and investigate the situations in which it can be harmful and sometimes even helpful. We further introduce novel corrective weights to remove bias when doing so is beneficial. Through this, our work not only provides a useful mechanism that can improve the active learning approach, but also an explanation for the empirical successes of various existing approaches which ignore this bias. In particular, we show that this bias can be actively helpful when training overparameterized models—like neural networks—with relatively modest dataset sizes.
Sebastian Farquhar, Yarin Gal, Tom Rainforth
ICLR, 2021 (Spotlight)
[Paper]
A Bayesian Perspective on Training Speed and Model Selection
We take a Bayesian perspective to illustrate a connection between training speed and the marginal likelihood in linear models. This provides two major insights: first, that a measure of a model’s training speed can be used to estimate its marginal likelihood. Second, that this measure, under certain conditions, predicts the relative weighting of models in linear model combinations trained to minimize a regression loss. We verify our results in model selection tasks for linear models and for the infinite-width limit of deep neural networks. We further provide encouraging empirical evidence that the intuition developed in these settings also holds for deep neural networks trained with stochastic gradient descent. Our results suggest a promising new direction towards explaining why neural networks trained with stochastic gradient descent are biased towards functions that generalize well.
Clare Lyle, Lisa Schut, Binxin (Robin) Ru, Yarin Gal, Mark van der Wilk
NeurIPS, 2020
[Paper] [Code] [BibTex]
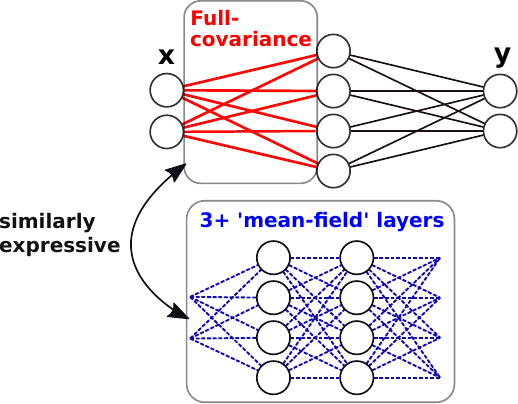
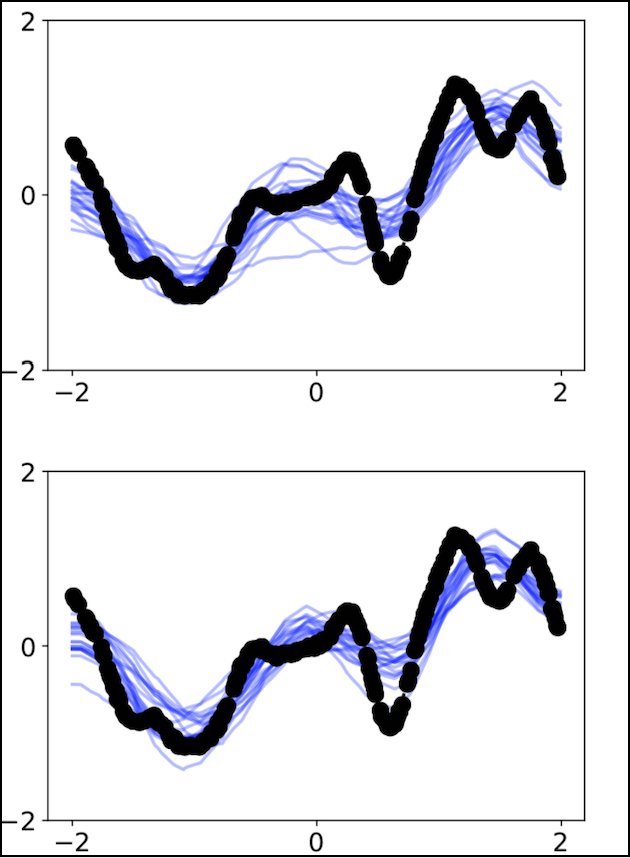
Liberty or Depth: Deep Bayesian Neural Nets Do Not Need Complex Weight Posterior Approximations
We challenge the longstanding assumption that the mean-field approximation for variational inference in Bayesian neural networks is severely restrictive, and show this is not the case in deep networks. We prove several results indicating that deep mean-field variational weight posteriors can induce similar distributions in function-space to those induced by shallower networks with complex weight posteriors. We validate our theoretical contributions empirically, both through examination of the weight posterior using Hamiltonian Monte Carlo in small models and by comparing diagonal- to structured-covariance in large settings. Since complex variational posteriors are often expensive and cumbersome to implement, our results suggest that using mean-field variational inference in a deeper model is both a practical and theoretically justified alternative to structured approximations.
Sebastian Farquhar, Lewis Smith, Yarin Gal
NeurIPS, 2020
[Paper] [arXiv]
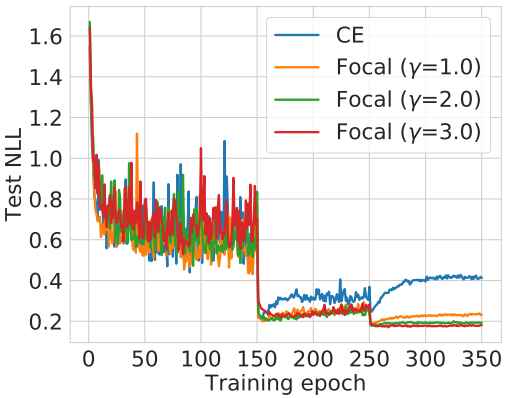
Calibrating Deep Neural Networks using Focal Loss
Miscalibration – a mismatch between a model’s confidence and its correctness – of Deep Neural Networks (DNNs) makes their predictions hard to rely on. Ideally, we want networks to be accurate, calibrated and confident. We show that, as opposed to the standard cross-entropy loss, focal loss (Lin et al., 2017) allows us to learn models that are already very well calibrated. When combined with temperature scaling, whilst preserving accuracy, it yields state-of-the-art calibrated models. We provide a thorough analysis of the factors causing miscalibration, and use the insights we glean from this to justify the empirically excellent performance of focal loss. To facilitate the use of focal loss in practice, we also provide a principled approach to automatically select the hyperparameter involved in the loss function. We perform extensive experiments on a variety of computer vision and NLP datasets, and with a wide variety of network architectures, and show that our approach achieves ... [full abstract]
Jishnu Mukhoti, Viveka Kulharia, Amartya Sanyal, Stuart Golodetz, Philip H.S. Torr, Puneet K. Dokania
NeurIPS, 2020
[Paper]
On using Focal Loss for Neural Network Calibration
Miscalibration – a mismatch between a model’s confidence and its correctness – of Deep Neural Networks (DNNs) makes their predictions hard to rely on. Ideally, we want networks to be accurate and calibrated. In this work, we study focal loss as an alternative to the conventional cross-entropy loss and show that, focal loss allows us to learn models that are comparitively well calibrated while preserving accuracy. We provide a thorough analysis of the factors causing miscalibration, and use the insights we glean from this to justify the superior performance of focal loss. Finally, we perform extensive experiments on a variety of datasets, and with a wide variety of network architectures, and show that focal loss indeed achieves excellent calibration without compromising on accuracy in almost all cases.
Jishnu Mukhoti, Viveka Kulharia, Amartya Sanyal, Stuart Golodetz, Philip H.S. Torr, Puneet K. Dokania
Uncertainty and Robustness in Deep Learning Workshop, ICML 2020
[Paper]
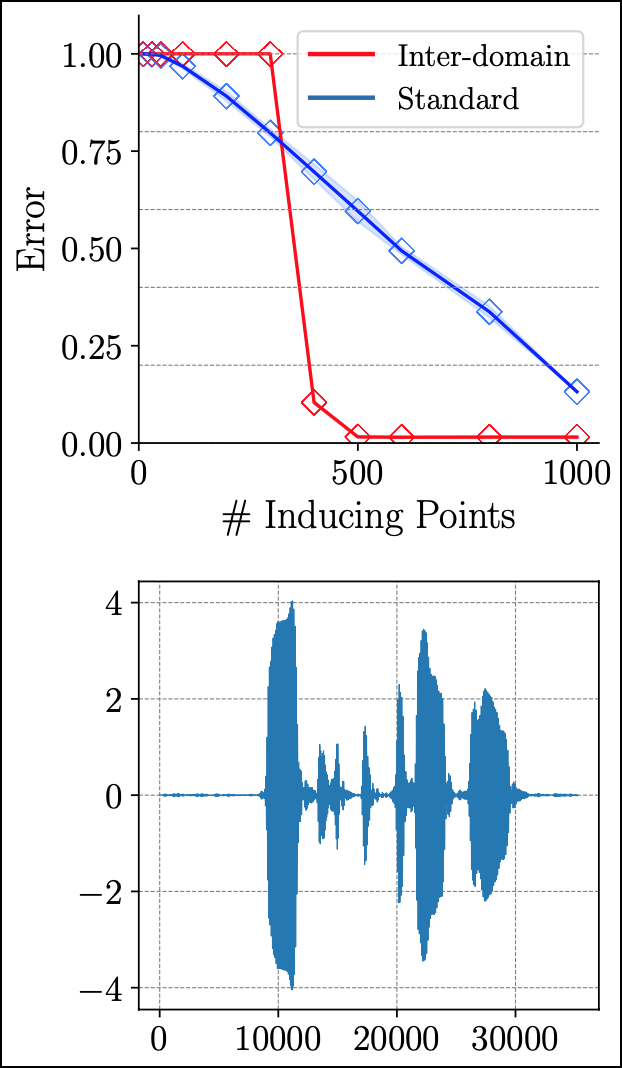
Inter-domain Deep Gaussian Processes
Inter-domain Gaussian processes (GPs) allow for high flexibility and low computational cost when performing approximate inference in GP models. They are particularly suitable for modeling data exhibiting global structure but are limited to stationary covariance functions and thus fail to model non-stationary data effectively. We propose Inter-domain Deep Gaussian Processes, an extension of inter-domain shallow GPs that combines the advantages of inter-domain and deep Gaussian processes (DGPs), and demonstrate how to leverage existing approximate inference methods to perform simple and scalable approximate inference using inter-domain features in DGPs. We assess the performance of our method on a range of regression tasks and demonstrate that it outperforms inter-domain shallow GPs and conventional DGPs on challenging large-scale real-world datasets exhibiting both global structure as well as a high-degree of non-stationarity.
Tim G. J. Rudner, Dino Sejdinovic, Yarin Gal
ICML, 2020
[arXiv] [Website] [Talk] [Slides] [BibTex]
Try Depth Instead of Weight Correlations: Mean-field is a Less Restrictive Assumption for Deeper Networks
We challenge the longstanding assumption that the mean-field approximation for variational inference in Bayesian neural networks is severely restrictive. We argue mathematically that full-covariance approximations only improve the ELBO if they improve the expected log-likelihood. We further show that deeper mean-field networks are able to express predictive distributions approximately equivalent to shallower full-covariance networks. We validate these observations empirically, demonstrating that deeper models decrease the divergence between diagonal- and full-covariance Gaussian fits to the true posterior.
Sebastian Farquhar, Lewis Smith, Yarin Gal
Contributed talk, Workshop on Bayesian Deep Learning, NeurIPS 2019
[Workshop paper], [arXiv]
Radial Bayesian Neural Networks: Beyond Discrete Support In Large-Scale Bayesian Deep Learning
We propose Radial Bayesian Neural Networks (BNNs): a variational approximate posterior for BNNs which scales well to large models while maintaining a distribution over weight-space with full support. Other scalable Bayesian deep learning methods, like MC dropout or deep ensembles, have discrete support—they assign zero probability to almost all of the weight-space. Unlike these discrete support methods, Radial BNNs’ full support makes them suitable for use as a prior for sequential inference. In addition, they solve the conceptual challenges with the a priori implausibility of weight distributions with discrete support. The Radial BNN is motivated by avoiding a sampling problem in ‘mean-field’ variational inference (MFVI) caused by the so-called ‘soap-bubble’ pathology of multivariate Gaussians. We show that, unlike MFVI, Radial BNNs are robust to hyperparameters and can be efficiently applied to a challenging real-world medical application without needing ad-hoc tweaks and inte... [full abstract]
Sebastian Farquhar, Michael Osborne, Yarin Gal
The 23rd International Conference on Artificial Intelligence and Statistics (AISTATS)
[arXiv]
On the Connection between Neural Processes and Gaussian Processes with Deep Kernels
Neural Processes (NPs) are a class of neural latent variable models that combine desirable properties of Gaussian Processes (GPs) and neural networks. Like GPs, NPs define distributions over functions and are able to estimate the uncertainty in their predictions. Like neural networks, NPs are computationally efficient during training and prediction time. We establish a simple and explicit connection between NPs and GPs. In particular, we show that, under certain conditions, NPs are mathematically equivalent to GPs with deep kernels. This result further elucidates the relationship between GPs and NPs and makes previously derived theoretical insights about GPs applicable to NPs. Furthermore, it suggests a novel approach to learning expressive GP covariance functions applicable across different prediction tasks by training a deep kernel GP on a set of datasets
Tim G. J. Rudner, Vincent Fortuin, Yee Whye Teh, Yarin Gal
NeurIPS Workshop on Bayesian Deep Learning, 2018
[Paper] [BibTex]
A Unifying Bayesian View of Continual Learning
Some machine learning applications require continual learning—where data comes in a sequence of datasets, each is used for training and then permanently discarded. From a Bayesian perspective, continual learning seems straightforward: Given the model posterior one would simply use this as the prior for the next task. However, exact posterior evaluation is intractable with many models, especially with Bayesian neural networks (BNNs). Instead, posterior approximations are often sought. Unfortunately, when posterior approximations are used, prior-focused approaches do not succeed in evaluations designed to capture properties of realistic continual learning use cases. As an alternative to prior-focused methods, we introduce a new approximate Bayesian derivation of the continual learning loss. Our loss does not rely on the posterior from earlier tasks, and instead adapts the model itself by changing the likelihood term. We call these approaches likelihood-focused. We then combine pri... [full abstract]
Sebastian Farquhar, Yarin Gal
NeurIPS 2018 workshop on Bayesian Deep Learning
[Paper] [BibTex]
BRUNO: A Deep Recurrent Model for Exchangeable Data
We present a novel model architecture which leverages deep learning tools to perform exact Bayesian inference on sets of high dimensional, complex observations. Our model is provably exchangeable, meaning that the joint distribution over observations is invariant under permutation: this property lies at the heart of Bayesian inference. The model does not require variational approximations to train, and new samples can be generated conditional on previous samples, with cost linear in the size of the conditioning set. The advantages of our architecture are demonstrated on learning tasks that require generalisation from short observed sequences while modelling sequence variability, such as conditional image generation, few-shot learning, and anomaly detection.
Iryna Korshunova, Jonas Degrave, Ferenc Huszár, Yarin Gal, Arthur Gretton, Joni Dambre
arXiv, 2018
[arXiv] [BibTex]
NIPS, 2018
[Paper] [BibTex]
Fast and Scalable Bayesian Deep Learning by Weight-Perturbation in Adam
Uncertainty computation in deep learning is essential to design robust and reliable systems. Variational inference (VI) is a promising approach for such computation, but requires more effort to implement and execute compared to maximum-likelihood methods. In this paper, we propose new natural-gradient algorithms to reduce such efforts for Gaussian mean-field VI. Our algorithms can be implemented within the Adam optimizer by perturbing the network weights during gradient evaluations, and uncertainty estimates can be cheaply obtained by using the vector that adapts the learning rate. This requires lower memory, computation, and implementation effort than existing VI methods, while obtaining uncertainty estimates of comparable quality. Our empirical results confirm this and further suggest that the weight-perturbation in our algorithm could be useful for exploration in reinforcement learning and stochastic optimization.
Mohammad Emtiyaz Khan, Didrik Nielsen, Voot Tangkaratt, Wu Lin, Yarin Gal, Akash Srivastava
ICML, 2018
[Paper] [arXiv] [BibTex]
Differentially private continual learning
Catastrophic forgetting can be a significant problem for institutions that must delete historic data for privacy reasons. For example, hospitals might not be able to retain patient data permanently. But neural networks trained on recent data alone will tend to forget lessons learned on old data. We present a differentially private continual learning framework based on variational inference. We estimate the likelihood of past data given the current model using differentially private generative models of old datasets. The differentially private training has no detrimental impact on our architecture’s continual learning performance, and still outperforms the current state-of-the-art non-private continual learning.
Sebastian Farquhar, Yarin Gal
Privacy in Machine Learning and Artificial Intelligence workshop, ICML, 2018
[Paper] [BibTex]
Loss-Calibrated Approximate Inference in Bayesian Neural Networks
Current approaches in approximate inference for Bayesian neural networks minimise the Kullback-Leibler divergence to approximate the true posterior over the weights. However, this approximation is without knowledge of the final application, and therefore cannot guarantee optimal predictions for a given task. To make more suitable task-specific approximations, we introduce a new loss-calibrated evidence lower bound for Bayesian neural networks in the context of supervised learning, informed by Bayesian decision theory. By introducing a lower bound that depends on a utility function, we ensure that our approximation achieves higher utility than traditional methods for applications that have asymmetric utility functions. Furthermore, in using dropout inference, we highlight that our new objective is identical to that of standard dropout neural networks, with an additional utility-dependent penalty term. We demonstrate our new loss-calibrated model with an illustrative medical examp... [full abstract]
Adam D. Cobb, Stephen J. Roberts, Yarin Gal
Theory of deep learning workshop, ICML, 2018
[arXiv] [Code] [BibTex]
Towards Robust Evaluations of Continual Learning
Continual learning experiments used in current deep learning papers do not faithfully assess fundamental challenges of learning continually, masking weak-points of the suggested approaches instead. We study gaps in such existing evaluations, proposing essential experimental evaluations that are more representative of continual learning’s challenges, and suggest a re-prioritization of research efforts in the field. We show that current approaches fail with our new evaluations and, to analyse these failures, we propose a variational loss which unifies many existing solutions to continual learning under a Bayesian framing, as either ‘prior-focused’ or ‘likelihood-focused’. We show that while prior-focused approaches such as EWC and VCL perform well on existing evaluations, they perform dramatically worse when compared to likelihood-focused approaches on other simple tasks.
Sebastian Farquhar, Yarin Gal
Lifelong Learning: A Reinforcement Learning Approach workshop, ICML, 2018
[arXiv] [BibTex]
Vprop: Variational Inference using RMSprop
Many computationally-efficient methods for Bayesian deep learning rely on continuous optimization algorithms, but the implementation of these methods requires significant changes to existing code-bases. In this paper, we propose Vprop, a method for variational inference that can be implemented with two minor changes to the off-the-shelf RMSprop optimizer. Vprop also reduces the memory requirements of Black-Box Variational Inference by half. We derive Vprop using the conjugate-computation variational inference method, and establish its connections to Newton’s method, natural-gradient methods, and extended Kalman filters. Overall, this paper presents Vprop as a principled, computationally-efficient, and easy-to-implement method for Bayesian deep learning.
Mohammad Emtiyaz Khan, Zuozhu Liu, Voot Tangkaratt, Yarin Gal
Bayesian Deep Learning workshop, NIPS, 2017
[Paper] [arXiv] [BibTex]

 All publications
All publications Bayesian Deep Learning
Bayesian Deep Learning Deep Learning
Deep Learning Inference
Inference
 Data Efficient AI
Data Efficient AI Adversarial and Interpretable ML
Adversarial and Interpretable ML Autonomous Driving
Autonomous Driving Reinforcement Learning
Reinforcement Learning Natural Language Processing
Natural Language Processing Space and Earth Observations
Space and Earth Observations Medical
Medical AI for Good and AI safety
AI for Good and AI safety