Back to all members...
Clare Lyle
PhD (2018—2023)

Clare was a DPhil student at the University of Oxford working with Yarin Gal and Marta Kwiatkowska. She has previously worked on developing a stronger theoretical understanding of distributional reinforcement learning at Google Brain, and is broadly interested in theoretical foundations of machine learning. She obtained her undergraduate degree in mathematics and computer science at McGill University, and was a Rhodes Scholar.
Publications while at OATML • News items mentioning Clare Lyle • Reproducibility and Code • Blog Posts
Publications while at OATML:
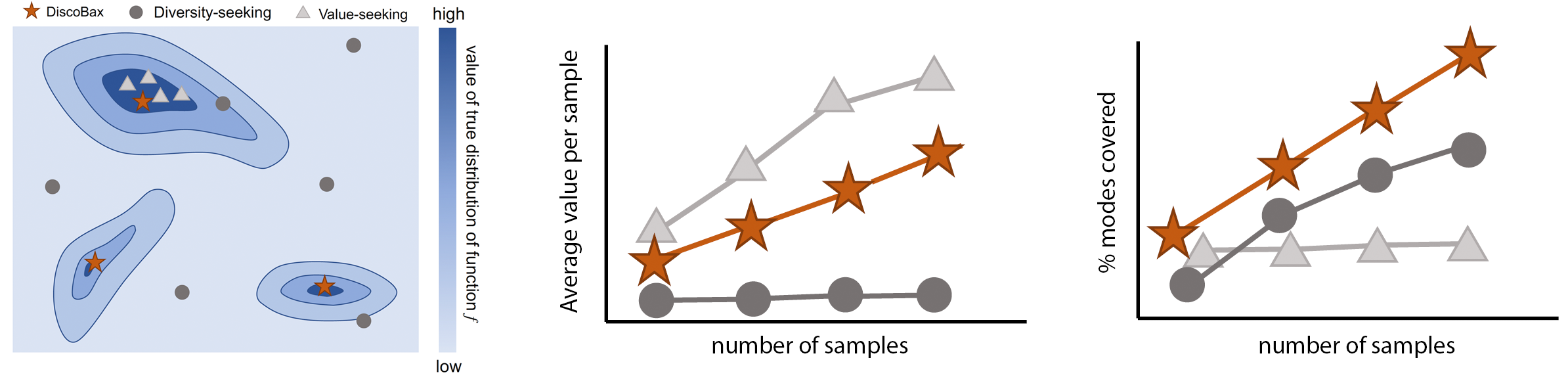
DiscoBAX - Discovery of optimal intervention sets in genomic experiment design
The discovery of novel therapeutics to cure genetic pathologies relies on the identification of the different genes involved in the underlying disease mechanism. With billions of potential hypotheses to test, an exhaustive exploration of the entire space of potential interventions is impossible in practice. Sample-efficient methods based on active learning or bayesian optimization bear the promise of identifying interesting targets using the least experiments possible. However, genomic perturbation experiments typically rely on proxy outcomes measured in biological model systems that may not completely correlate with the outcome of interventions in humans. In practical experiment design, one aims to find a set of interventions which maximally move a target phenotype via a diverse set of mechanisms in order to reduce the risk of failure in future stages of trials. To that end, we introduce DiscoBAX — a sample-efficient algorithm for the discovery of genetic interventions that maxim... [full abstract]
Clare Lyle, Arash Mehrjou, Pascal Notin, Andrew Jesson, Stefan Bauer, Yarin Gal, Patrick Schwab
ICML 2023
[arXiv]
Learning Dynamics and Generalization in Deep Reinforcement Learning
Solving a reinforcement learning (RL) problem poses two competing challenges: fitting a potentially discontinuous value function, and generalizing well to new observations. In this paper, we analyze the learning dynamics of temporal difference algorithms to gain novel insight into the tension between these two objectives. We show theoretically that temporal difference learning encourages agents to fit non-smooth components of the value function early in training, and at the same time induces the second-order effect of discouraging generalization. We corroborate these findings in deep RL agents trained on a range of environments, finding that neural networks trained using temporal difference algorithms on dense reward tasks exhibit weaker generalization between states than randomly initialized networks and networks trained with policy gradient methods. Finally, we investigate how post-training policy distillation may avoid this pitfall, and show that this approach improves generaliz... [full abstract]
Clare Lyle, Mark Rowland, Will Dabney, Marta Kwiatkowska, Yarin Gal
ICML
[paper]
[poster]
Understanding and Preventing Capacity Loss in Reinforcement Learning
The reinforcement learning (RL) problem is rife with sources of non-stationarity that can destabilize or inhibit learning progress. We identify a key mechanism by which this occurs in agents using neural networks as function approximators: capacity loss, whereby networks trained to predict a sequence of target values lose their ability to quickly fit new functions over time. We demonstrate that capacity loss occurs in a broad range of RL agents and environments, and is particularly damaging to learning progress in sparse-reward tasks. We then present a simple regularizer, Initial Feature Regularization (InFeR), that mitigates this phenomenon by regressing a subspace of features towards its value at initialization, improving performance over a state-of-the-art model-free algorithm in the Atari 2600 suite. Finally, we study how this regularization affects different notions of capacity and evaluate other mechanisms by which it may improve performance.
Clare Lyle, Mark Rowland, Will Dabney
International Conference on Learning Representations, 2022
[arXiv] [BibTex]
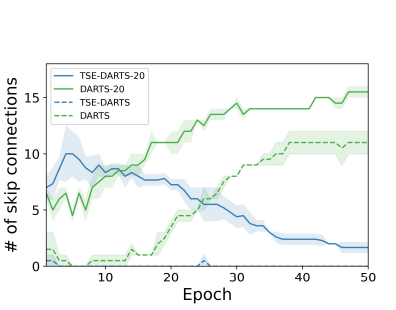
DARTS without a Validation Set; Optimizing the Marginal Likelihood
The success of neural architecture search (NAS) has historically been limited by excessive compute requirements. While modern weight-sharing NAS methods such as DARTS are able to finish the search in single-digit GPU days, extracting the final best architecture from the shared weights is notoriously unreliable. Training-Speed-Estimate (TSE), a recently developed generalization estimator with a Bayesian marginal likelihood interpretation, has previously been used in place of the validation loss for gradient-based optimization in DARTS. This prevents the DARTS skip connection collapse, which significantly improves performance on NASBench-201 and the original DARTS search space. We extend those results by applying various DARTS diagnostics and show several unusual behaviors arising from not using a validation set. Furthermore, our experiments yield concrete examples of the depth gap and topology selection in DARTS having a strongly negative impact on the search performance despite gen... [full abstract]
Miroslav Fil, Binxin (Robin) Ru, Clare Lyle, Yarin Gal
5th Workshop on Meta-Learning, NeurIPS 2021
[Paper]
Speedy Performance Estimation for Neural Architecture Search
Reliable yet efficient evaluation of generalisation performance of a proposed architecture is crucial to the success of neural architecture search (NAS). Traditional approaches face a variety of limitations: training each architecture to completion is prohibitively expensive, early stopped validation accuracy may correlate poorly with fully trained performance, and model-based estimators require large training sets. We instead propose to estimate the final test performance based on a simple measure of training speed. Our estimator is theoretically motivated by the connection between generalisation and training speed, and is also inspired by the reformulation of a PAC-Bayes bound under the Bayesian setting. Our model-free estimator is simple, efficient, and cheap to implement, and does not require hyperparameter-tuning or surrogate training before deployment. We demonstrate on various NAS search spaces that our estimator consistently outperforms other alternatives in achieving bette... [full abstract]
Binxin (Robin) Ru, Clare Lyle, Lisa Schut, Miroslav Fil, Mark van der Wilk, Yarin Gal
NeurIPS 2021
[Paper]
Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learning
We challenge a common assumption underlying most supervised deep learning: that a model makes a prediction depending only on its parameters and the features of a single input. To this end, we introduce a general-purpose deep learning architecture that takes as input the entire dataset instead of processing one datapoint at a time. Our approach uses self-attention to reason about relationships between datapoints explicitly, which can be seen as realizing non-parametric models using parametric attention mechanisms. However, unlike conventional non-parametric models, we let the model learn end-to-end from the data how to make use of other datapoints for prediction. Empirically, our models solve cross-datapoint lookup and complex reasoning tasks unsolvable by traditional deep learning models. We show highly competitive results on tabular data, early results on CIFAR-10, and give insight into how the model makes use of the interactions between points.
Jannik Kossen, Neil Band, Clare Lyle, Aidan Gomez, Yarin Gal, Tom Rainforth
NeurIPS, 2021
[OpenReview] [arXiv] [Code]
Resolving Causal Confusion in Reinforcement Learning via Robust Exploration
A reinforcement learning agent must distinguish between spurious correlations and causal relationships in its environment in order to robustly achieve its goals. Causal confusion has been defined and studied in various constrained settings, like imitation learning and the partial observability setting with latent confounders. We now show that causal confusion can also occur in online reinforcement learning (RL) settings. We formalize the problem of identifying causal structure in a Markov Decision Process and highlight the central role played by the data collection policy in identifying and avoiding spurious correlations. We find that under insufficient exploration, many RL algorithms, including those with PAC-MDP guarantees, fall prey to causal confusion under insufficient exploration policies. To address this, we present a robust exploration strategy which enables causal hypothesis-testing by interaction with the environment. Our method outperforms existing state-of-the-art a... [full abstract]
Clare Lyle, Amy Zhang, Minqui Jiang, Joelle Pineau, Yarin Gal
Self-Supervision for Reinforcement Learning Workshop-ICLR 2021
[Paper]
Provable Guarantees on the Robustness of Decision Rules to Causal Interventions
Robustness of decision rules to shifts in the data-generating process is crucial to the successful deployment of decision-making systems. Such shifts can be viewed as interventions on a causal graph, which capture (possibly hypothetical) changes in the data-generating process, whether due to natural reasons or by the action of an adversary. We consider causal Bayesian networks and formally define the interventional robustness problem, a novel model-based notion of robustness for decision functions that measures worst-case performance with respect to a set of interventions that denote changes to parameters and/or causal influences. By relying on a tractable representation of Bayesian networks as arithmetic circuits, we provide efficient algorithms for computing guaranteed upper and lower bounds on the interventional robustness probabilities. Experimental results demonstrate that the methods yield useful and interpretable bounds for a range of practical networks, paving the way towar... [full abstract]
Benjie Wang, Clare Lyle, Marta Kwiatkowska
IJCAI, 2021
[Paper]
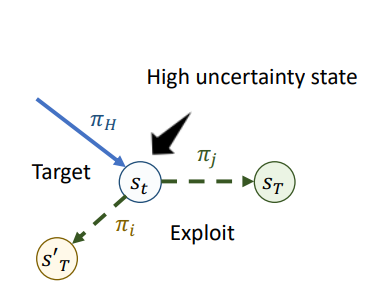
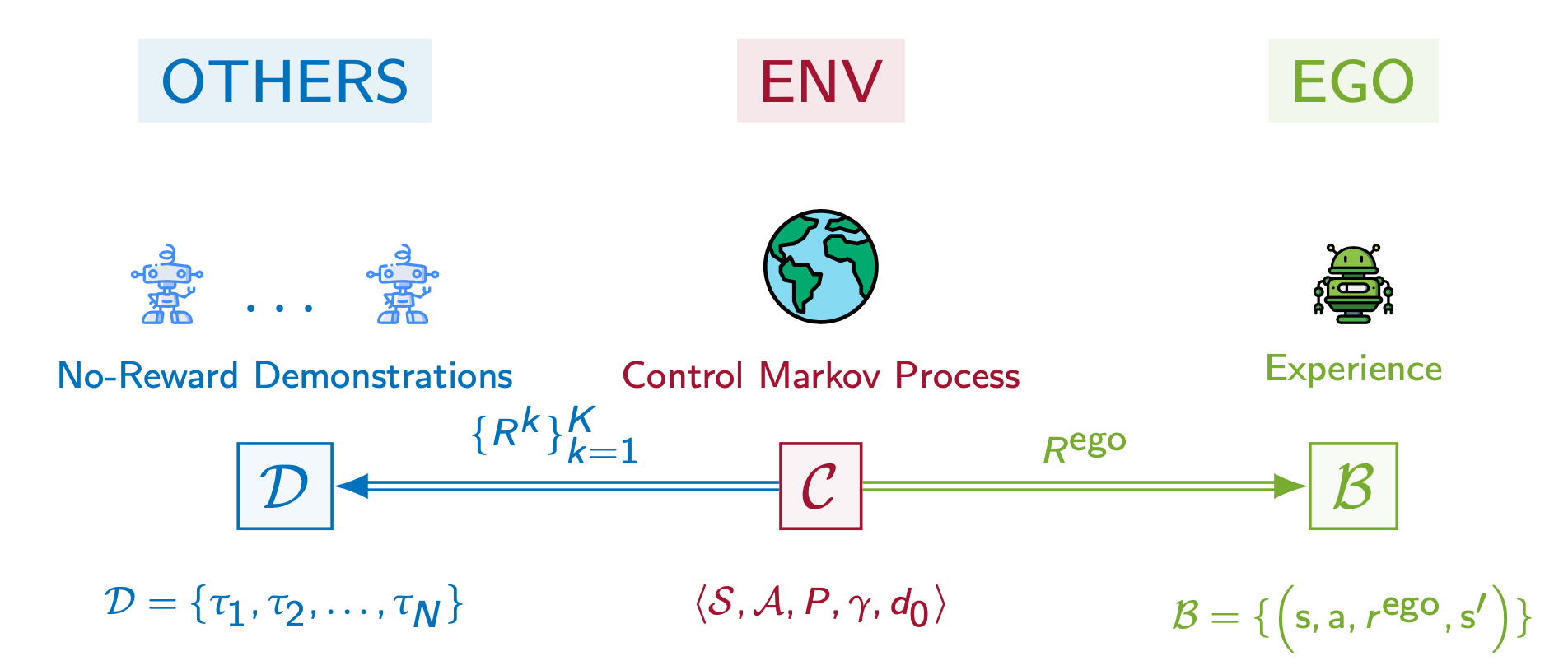
PsiPhi-Learning: Reinforcement Learning with Demonstrations using Successor Features and Inverse Temporal Difference Learning
We study reinforcement learning (RL) with no-reward demonstrations, a setting in which an RL agent has access to additional data from the interaction of other agents with the same environment. However, it has no access to the rewards or goals of these agents, and their objectives and levels of expertise may vary widely. These assumptions are common in multi-agent settings, such as autonomous driving. To effectively use this data, we turn to the framework of successor features. This allows us to disentangle shared features and dynamics of the environment from agent-specific rewards and policies. We propose a multi-task inverse reinforcement learning (IRL) algorithm, called _inverse temporal difference learning_ (ITD), that learns shared state features, alongside per-agent successor features and preference vectors, purely from demonstrations without reward labels. We further show how to seamlessly integrate ITD with learning from online environment interactions, arriving at a novel a... [full abstract]
Angelos Filos, Clare Lyle, Yarin Gal, Sergey Levine, Natasha Jaques, Gregory Farquhar
ICML, 2021 (long talk)
[Paper]
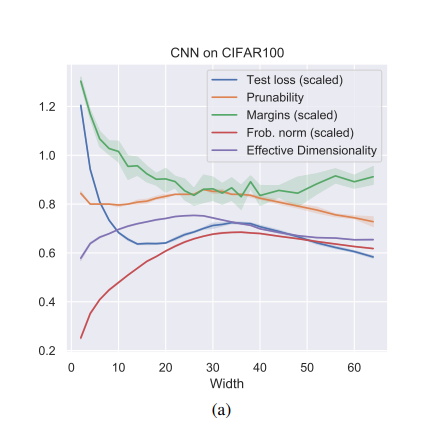
Robustness to Pruning Predicts Generalization in Deep Neural Networks
Existing generalization measures that aim to capture a model's simplicity based on parameter counts or norms fail to explain generalization in overparameterized deep neural networks. In this paper, we introduce a new, theoretically motivated measure of a network's simplicity which we call prunability: the smallest \emph{fraction} of the network's parameters that can be kept while pruning without adversely affecting its training loss. We show that this measure is highly predictive of a model's generalization performance across a large set of convolutional networks trained on CIFAR-10, does not grow with network size unlike existing pruning-based measures, and exhibits high correlation with test set loss even in a particularly challenging double descent setting. Lastly, we show that the success of prunability cannot be explained by its relation to known complexity measures based on models' margin, flatness of minima and optimization speed, finding that our new measure is similar to -... [full abstract]
Lorenz Kuhn, Clare Lyle, Aidan Gomez, Jonas Rothfuss, Yarin Gal
arXiv
[paper]
On the Effect of Auxiliary Tasks on Representation Dynamics
While auxiliary tasks play a key role in shaping the representations learnt by reinforcement learning agents, much is still unknown about the mechanisms through which this is achieved. This work develops our understanding of the relationship between auxiliary tasks, environment structure, and representations by analysing the dynamics of temporal difference algorithms. Through this approach, we establish a connection between the spectral decomposition of the transition operator and the representations induced by a variety of auxiliary tasks. We then leverage insights from these theoretical results to inform the selection of auxiliary tasks for deep reinforcement learning agents in sparse-reward environments.
Clare Lyle, Mark Rowland, Georg Ostrovski, Will Dabney
AISTATS 2021
[paper]
A Bayesian Perspective on Training Speed and Model Selection
We take a Bayesian perspective to illustrate a connection between training speed and the marginal likelihood in linear models. This provides two major insights: first, that a measure of a model's training speed can be used to estimate its marginal likelihood. Second, that this measure, under certain conditions, predicts the relative weighting of models in linear model combinations trained to minimize a regression loss. We verify our results in model selection tasks for linear models and for the infinite-width limit of deep neural networks. We further provide encouraging empirical evidence that the intuition developed in these settings also holds for deep neural networks trained with stochastic gradient descent. Our results suggest a promising new direction towards explaining why neural networks trained with stochastic gradient descent are biased towards functions that generalize well.
Clare Lyle, Lisa Schut, Binxin (Robin) Ru, Yarin Gal, Mark van der Wilk
NeurIPS, 2020
[Paper] [Code] [BibTex]
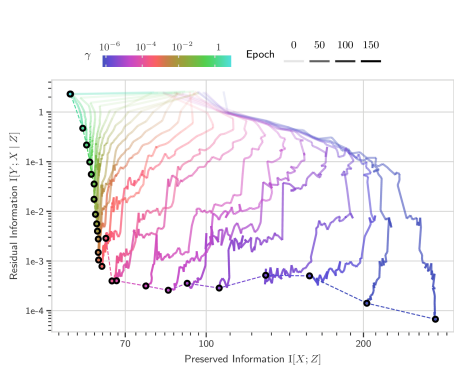
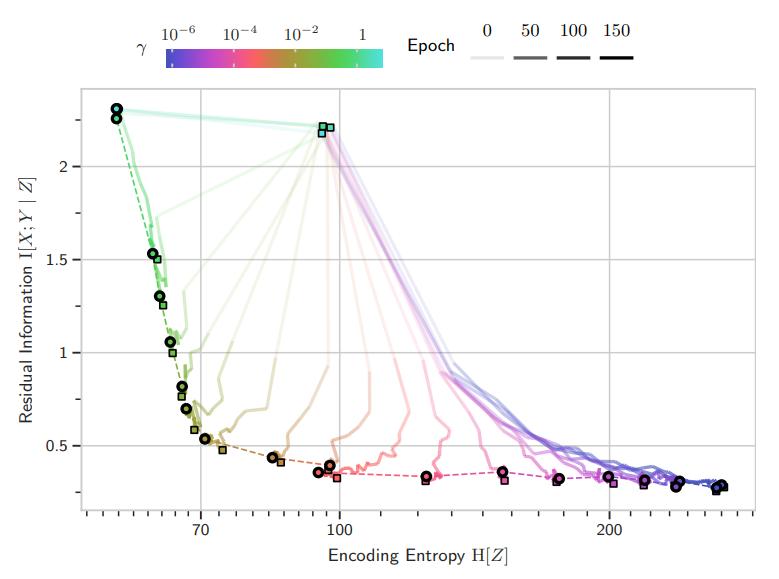
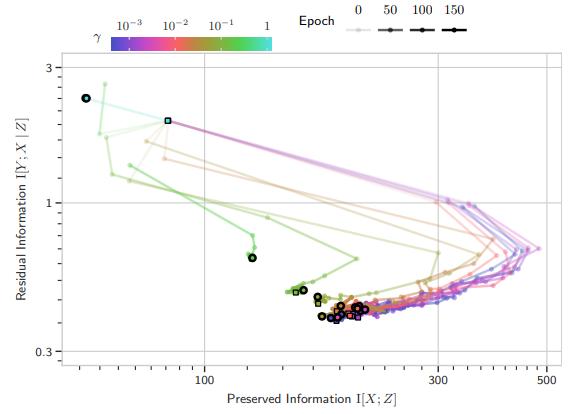
Scalable Training with Information Bottleneck Objectives
The Information Bottleneck principle offers both a mechanism to explain how deep neural networks train and generalize, as well as a regularized objective with which to train models, with multiple competing objectives proposed in the literature. Moreover, the information-theoretic quantities used in these objectives are difficult to compute for large deep neural networks, often relying on density estimation using generative models. This, in turn, limits their use as a training objective. In this work, we review these quantities, compare and unify previously proposed objectives and relate them to surrogate objectives more friendly to optimization without relying on cumbersome tools such as density estimation. We find that these surrogate objectives allow us to apply the information bottleneck to modern neural network architectures with stochastic latent representations. We demonstrate our insights on MNIST and CIFAR10 with modern neural network architectures..
Andreas Kirsch, Clare Lyle, Yarin Gal
ICML workshop on Uncertainty & Robustness in Deep Learning
[paper]
Unpacking Information Bottlenecks: Unifying Information-Theoretic Objectives in Deep Learning
The Information Bottleneck principle offers both a mechanism to explain how deep neural networks train and generalize, as well as a regularized objective with which to train models. However, multiple competing objectives are proposed in the literature, and the information-theoretic quantities used in these objectives are difficult to compute for large deep neural networks, which in turn limits their use as a training objective. In this work, we review these quantities and compare and unify previously proposed objectives, which allows us to develop surrogate objectives more friendly to optimization without relying on cumbersome tools such as density estimation. We find that these surrogate objectives allow us to apply the information bottleneck to modern neural network architectures. We demonstrate our insights on MNIST, CIFAR-10 and Imagenette with modern DNN architectures (ResNets).
Andreas Kirsch, Clare Lyle, Yarin Gal
Uncertainty & Robustness in Deep Learning Workshop, ICML, 2020
[Paper] [BibTex] [Poster]
Learning CIFAR-10 with a Simple Entropy Estimator Using Information Bottleneck Objectives
The Information Bottleneck (IB) principle characterizes learning and generalization in deep neural networks in terms of the change in two information theoretic quantities and leads to a regularized objective function for training neural networks. These quantities are difficult to compute directly for deep neural networks. We show that it is possible to backpropagate through a simple entropy estimator to obtain an IB training method that works for modern neural network architectures. We evaluate our approach empirically on the CIFAR-10 dataset, showing that IB objectives can yield competitive performance on this dataset with a conceptually simple approach while also performing well against adversarial attacks out-of-the-box.
Andreas Kirsch, Clare Lyle, Yarin Gal
Uncertainty & Robustness in Deep Learning Workshop, ICML, 2020
[Paper] [BibTex]
Invariant Causal Prediction for Block MDPs
Generalization across environments is critical to the successful application of reinforcement learning algorithms to real-world challenges. In this paper, we consider the problem of learning abstractions that generalize in block MDPs, families of environments with a shared latent state space and dynamics structure over that latent space, but varying observations. We leverage tools from causal inference to propose a method of invariant prediction to learn model-irrelevance state abstractions (MISA) that generalize to novel observations in the multi-environment setting. We prove that for certain classes of environments, this approach outputs with high probability a state abstraction corresponding to the causal feature set with respect to the return. We further provide more general bounds on model error and generalization error in the multi-environment setting, in the process showing a connection between causal variable selection and the state abstraction framework for MDPs. We give e... [full abstract]
Amy Zhang, Clare Lyle, Shagun Sodhani, Angelos Filos, Marta Kwiatkowska, Joelle Pineau, Yarin Gal, Doina Precup
Causal Learning for Decision Making Workshop at ICLR, 2020
[Paper]
ICML, 2020
[Paper]
PAC-Bayes Generalization Bounds for Invariant Neural Networks
Invariance is widely described as a desirable property of neural networks, but the mechanisms by which it benefits deep learning remain shrouded in mystery. We show that building invariance into model architecture via feature averaging provably tightens PAC-Bayes generalization bounds, as compared to data augmentation. Furthermore, through a link to the marginal likelihood and Bayesian model selection, we provide justification for using the improvement in these bounds for model selection. Our key observation is that invariance doesn't just reduce variance in deep learning: it also changes the parameter-function mapping, and this leads better provable guarantees for the model. We verify our theoretical results empirically on a permutation-invariant dataset.
Clare Lyle, Marta Kwiatkowska, Yarin Gal
14th Women in Machine Learning Workshop (WiML 2019)
[WiML]
A Geometric Perspective on Optimal Representations for Reinforcement Learning
We propose a new perspective on representation learning in reinforcement learning based on geometric properties of the space of value functions. We leverage this perspective to provide formal evidence regarding the usefulness of value functions as auxiliary tasks. Our formulation considers adapting the representation to minimize the (linear) approximation of the value function of all stationary policies for a given environment. We show that this optimization reduces to making accurate predictions regarding a special class of value functions which we call adversarial value functions (AVFs). We demonstrate that using value functions as auxiliary tasks corresponds to an expected-error relaxation of our formulation, with AVFs a natural candidate, and identify a close relationship with proto-value functions (Mahadevan, 2005). We highlight characteristics of AVFs and their usefulness as auxiliary tasks in a series of experiments on the four-room domain.
Marc G. Bellemare, Will Dabney, Robert Dadashi, Adrien Ali Taiga, Pablo Samuel Castro, Nicolas Le Roux, Dale Schuurmans, Tor Lattimore, Clare Lyle
NeurIPS, 2019
[arXiv]
An Analysis of the Effect of Invariance on Generalization in Neural Networks
Invariance is often cited as a desirable property of machine learning systems, claimed to improve model accuracy and reduce overfitting. Empirically, invariant models often generalize better than their non-invariant counterparts. But is it possible to show that invariant models provably do so? In this paper we explore the effect of invariance on model generalization. We find strong Bayesian and frequentist motivations for enforcing invariance which leverage recent results connecting PAC-Bayes generalization bounds and the marginal likelihood. We make use of these results to perform model selection on neural networks.
Clare Lyle, Marta Kwiatkowska, Mark van der Wilk, Yarin Gal
Understanding and Improving Generalization in Deep Learning workshop, ICML, 2019
[Paper]
A Comparative Analysis of Distributional and Expected Reinforcement Learning
Since their introduction a year ago, distributional approaches to reinforcement learning (distributional RL) have produced strong results relative to the standard approach which models expected values (expected RL). However, aside from convergence guarantees, there have been few theoretical results investigating the reasons behind the improvements distributional RL provides. In this paper we begin the investigation into this fundamental question by analyzing the differences in the tabular, linear approximation, and non-linear approximation settings. We prove that in many realizations of the tabular and linear approximation settings, distributional RL behaves exactly the same as expected RL. In cases where the two methods behave differently, distributional RL can in fact hurt performance when it does not induce identical behaviour. We then continue with an empirical analysis comparing distributional and expected RL methods in control settings with non-linear approximators to tease a... [full abstract]
Clare Lyle, Pablo Samuel Castro, Marc G Bellemare
AAAI 2019
[Paper]
The Malicious Use of Artificial Intelligence - Forecasting, Prevention, and Mitigation
This report surveys the landscape of potential security threats from malicious uses of AI, and proposes ways to better forecast, prevent, and mitigate these threats. After analyzing the ways in which AI may influence the threat landscape in the digital, physical, and political domains, we make four high-level recommendations for AI researchers and other stakeholders. We also suggest several promising areas for further research that could expand the portfolio of defenses, or make attacks less effective or harder to execute. Finally, we discuss, but do not conclusively resolve, the long-term equilibrium of attackers and defenders.
Miles Brundage, Shahar Avin, Jack Clark, Helen Toner, Peter Eckersley, Ben Garfinkel, Allan Dafoe, Paul Scharre, Thomas Zeitzoff, Bobby Filar, Hyrum Anderson, Heather Roff, Gregory C. Allen, Jacob Steinhardt, Carrick Flynn, Seán Ó hÉigeartaigh, Simon Beard, Haydn Belfield, Sebastian Farquhar, Clare Lyle, Rebecca Crootof, Owain Evans, Michael Page, Joanna Bryson, Roman Yampolskiy, Dario Amodei
arXiv
[report]
News items mentioning Clare Lyle:

OATML to co-organize the Machine Learning for Drug Discovery (MLDD) workshop at ICLR 2023
21 Dec 2022
OATML students Pascal Notin and Clare Lyle, along with OATML group leader Yarin Gal, are co-organizing the Machine Learning for Drug Discovery (MLDD) workshop at ICLR 2023 jointly with collaborators at GSK, Genentech, Harvard, MIT and others. OATML students Neil Band, Freddie Bickford Smith, Jan Brauner, Lars Holdijk, Andrew Jesson, Andreas Kirsch, Shreshth Malik, Lood van Niekirk and Ruben Wietzman are part of the program committee.

OATML graduate students recognized as highlighted reviewers at ICLR 2022
25 Apr 2022
OATML graduate students Lars Holdijk, Jannik Kossen, Clare Lyle, and Sören Mindermann are recognized as Highlighted Reviewers for their reviewing at ICLR 2022.

OATML to co-organize the Machine Learning for Drug Discovery (MLDD) workshop at ICLR 2022
15 Jan 2022
OATML students Pascal Notin, Andrew Jesson and Clare Lyle, along with OATML group leader Professor Yarin Gal, are co-organizing the first Machine Learning for Drug Discovery (MLDD) workshop at ICLR 2022 jointly with collaborators at GSK, Harvard, MILA, MIT and others. OATML students Neil Band, Freddie Bickford Smith, Jan Brauner, Lars Holdijk, Andreas Kirsch, Jannik Kossen and Muhammed Razzak are part of the PC.

NeurIPS 2021
11 Oct 2021
Thirteen papers with OATML members accepted to NeurIPS 2021 main conference. More information in our blog post.

OATML researchers to present at Stanford University Lecture Course CS25: Transformers United
22 Aug 2021
OATML graduate students Aidan Gomez, Jannik Kossen, and Neil Band will be presenting their recent paper Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learning that introduces Non-Parametric Transformers at the Stanford Lecture Course ‘CS25: Transformers United’ on November 1, 2021. Professor Yarin Gal, Dr. Tom Rainforth, and OATML DPhil student Clare Lyle are co-authors on the paper.
The lecture is available online here.

OATML researchers to speak at Google Research
22 Aug 2021
OATML students Jannik Kossen and Neil Band will be presenting their recent paper Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learning at Google Research on September 14, 2021. Professor Yarin Gal, Dr. Tom Rainforth, and OATML DPhil students Clare Lyle and Aidan Gomez are co-authors on the paper.

OATML researcher presents at AI Campus Berlin
06 Aug 2021
OATML DPhil student Jannik Kossen gives invited talks at AI Campus Berlin on two recent papers: Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learning and Active Testing: Sample-Efficient Model Evaluation. Recordings of are available upon request. Announcements are here and here. Professor Yarin Gal, Dr. Tom Rainforth, and OATML graduate students Sebastian Farquhar, Neil Band, Clare Lyle, and Aidan Gomez are co-authors on the papers.

ICML 2021
17 Jul 2021
Seven papers with OATML members accepted to ICML 2021, together with 14 workshop papers. More information in our blog post.

OATML researchers to speak at Cohere
09 Jul 2021
OATML students Jannik Kossen and Neil Band present their recent paper Self-Attention Between Datapoints: Going Beyond Individual Input-Output Pairs in Deep Learning at Cohere on July 9, 2021. Professor Yarin Gal, Dr. Tom Rainforth, and OATML DPhil students Clare Lyle and Aidan Gomez are also co-authors on the paper.
OATML researcher invited to speak at Simons Institute
29 Sep 2020
OATML graduate student Clare Lyle will be giving a talk about her work with Professor Yarin Gal on causal inference and generalization in deep reinforcement learning at the Simons Institute Workshop on Deep Reinforcement Learning on Thursday October 1.

Clare Lyle awarded OpenPhil AI Fellowship
09 Jun 2020
OATML graduate student Clare Lyle has been selected for the 2020 Open Philanthropy AI Fellowship. The fellowship will support her research for five years.
Blog Posts
OATML at ICLR 2022
OATML group members and collaborators are proud to present 4 papers at ICLR 2022 main conference. …
Full post...Yarin Gal, Tuan Nguyen, Andrew Jesson, Pascal Notin, Atılım Güneş Baydin, Clare Lyle, Milad Alizadeh, Joost van Amersfoort, Sebastian Farquhar, Muhammed Razzak, Freddie Kalaitzis, 01 Feb 2022
13 OATML Conference papers at NeurIPS 2021
OATML group members and collaborators are proud to present 13 papers at NeurIPS 2021 main conference. …
Full post...Jannik Kossen, Neil Band, Aidan Gomez, Clare Lyle, Tim G. J. Rudner, Yarin Gal, Binxin (Robin) Ru, Clare Lyle, Lisa Schut, Atılım Güneş Baydin, Tim G. J. Rudner, Andrew Jesson, Panagiotis Tigas, Joost van Amersfoort, Andreas Kirsch, Pascal Notin, Angelos Filos, 11 Oct 2021
21 OATML Conference and Workshop papers at ICML 2021
OATML group members and collaborators are proud to present 21 papers at ICML 2021, including 7 papers at the main conference and 14 papers at various workshops. Group members will also be giving invited talks and participate in panel discussions at the workshops. …
Full post...Angelos Filos, Clare Lyle, Jannik Kossen, Sebastian Farquhar, Tom Rainforth, Andrew Jesson, Sören Mindermann, Tim G. J. Rudner, Oscar Key, Binxin (Robin) Ru, Pascal Notin, Panagiotis Tigas, Andreas Kirsch, Jishnu Mukhoti, Joost van Amersfoort, Lisa Schut, Muhammed Razzak, Aidan Gomez, Jan Brauner, Yarin Gal, 17 Jul 2021
22 OATML Conference and Workshop papers at NeurIPS 2020
OATML group members and collaborators are proud to be presenting 22 papers at NeurIPS 2020. Group members are also co-organising various events around NeurIPS, including workshops, the NeurIPS Meet-Up on Bayesian Deep Learning and socials. …
Full post...Muhammed Razzak, Panagiotis Tigas, Angelos Filos, Atılım Güneş Baydin, Andrew Jesson, Andreas Kirsch, Clare Lyle, Freddie Kalaitzis, Jan Brauner, Jishnu Mukhoti, Lewis Smith, Lisa Schut, Mizu Nishikawa-Toomey, Oscar Key, Binxin (Robin) Ru, Sebastian Farquhar, Sören Mindermann, Tim G. J. Rudner, Yarin Gal, 04 Dec 2020
13 OATML Conference and Workshop papers at ICML 2020
We are glad to share the following 13 papers by OATML authors and collaborators to be presented at this ICML conference and workshops …
Full post...Angelos Filos, Sebastian Farquhar, Tim G. J. Rudner, Lewis Smith, Lisa Schut, Tom Rainforth, Panagiotis Tigas, Pascal Notin, Andreas Kirsch, Clare Lyle, Joost van Amersfoort, Jishnu Mukhoti, Yarin Gal, 10 Jul 2020
25 OATML Conference and Workshop papers at NeurIPS 2019
We are glad to share the following 25 papers by OATML authors and collaborators to be presented at this NeurIPS conference and workshops. …
Full post...Angelos Filos, Sebastian Farquhar, Aidan Gomez, Tim G. J. Rudner, Zac Kenton, Lewis Smith, Milad Alizadeh, Tom Rainforth, Panagiotis Tigas, Andreas Kirsch, Clare Lyle, Joost van Amersfoort, Yarin Gal, 08 Dec 2019
An imPACtful, BAYESic result
The applications of probably approximately correct (PAC) learning results to deep networks have historically been about as interesting as they sound. For neural networks of the scale used in practical applications, bounds involving concepts like VC dimension conclude that the algorithm will have no more than a certain error rate on the test set with probability at least zero. Recently, some work by Dziugaite and Roy, along with some folks from Columbia has managed to obtain non-vacuous generalization bounds for more realistic problems using a concept introduced by McAllester (1999) called PAC Bayes bounds. …
Full post...Clare Lyle, 09 Apr 2019